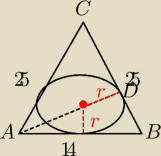
planimetria salv: W trójkąt równoramienny ABC o podstawie długości |AB | = 14 i polu 168 wpisano okrąg. Oblicz długość odcinka łączącego wierzchołek A z punktem wspólnym okręgu i ramienia BC. Czy w rysunku do tego zadania odcinek laczacy wierzcholek A z punktem wspolnym okregu i ramienia BC będzie przechodził przez środek i pokrywał się z promieniem okregu ?

Maciess: https://www.geogebra.org/graphing/dewccskk wynika z konstrukcji

iteRacj@: Chyba nie, zmieniłam trochę proporcje trójkąta, żeby mniej przypominał równoboczny. https://www.geogebra.org/graphing/uzsfxqrk

Maciess: zrobiłem jeden do jeden i za bardzo sie zasugerowałem

salv: https://www.zadania.info/d648/7282676 bo tak patrzę na to rozwiązanie,i ta dlugosc 7 jest wyznaczana przez styczne i promien,a promien pada pod katem prostym do stycznej a ten odcinek AD chyba sie nie pokrywa z promieniem

iteRacj@: Chyba chodzi o to, czy do odcinka AD należy środek okręgu. Nie należy.