Czy kwadrat o P=81 dm^2 wystarczy do sklejenia czworościanu foremnego o P=18 dm2
jezowj : Witam. Ponownie potrzebuję pomocy w zadaniu:
Czy kwadratowy arkusz brystolu o polu powierzchni równym 81 dm2 wystarczy aby skleić model
czworościanu foremnego o polu powierzchni całkowitej równym 18 dm2 ?
Wiem, że brystolu wystarczy (wynika to z mojego rysunku). Nie wiem w jaki sposób to obliczyć,
od czego zacząć.
30 mar 09:31
wredulus_pospolitus:
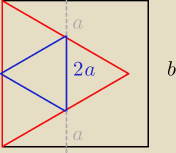
masz podane P
c czworościanu, więc wiesz znasz długość krawędzi tegoż czworościanu foremnego
(2a)
znasz P brystolu więc znasz długość boku (b)
jeszcze b ≥ 4a to wystarczy
30 mar 09:38
wredulus_pospolitus:
można też prościej
ów czerwony trójkąt ( 'rozłozony czworościan' ) ma powierzchnie 18dm
2 ... w takim razie jaką
długość ma jego bok
30 mar 09:39
wredulus_pospolitus:
PS ... tak naprawdę ten rysunek nie prezentuje ułożenia siatki czworościanu foremnego o
największej powierzchni, który można wyciąć z kwadratowego brystolu
30 mar 09:43
jezowj : Otrzymałem dziwny wynik długości boku a czworościanu.
30 mar 09:46
wredulus_pospolitus:
co to znaczy 'dziwny' wynik
30 mar 09:56
wredulus_pospolitus:
| | (4a)2√3 | | 9*4*2 | |
PΔ = 18 dm2 = |
| −> (4a)2 = |
| −> |
| | 4 | | √3 | |
| | 3*2*√2*4√27 | |
−> 4a = |
| = 24√44√27 = 24√52 < 24√81 = 2*3 = 6 |
| | 3 | |
wniosek
30 mar 10:01
jezowj: wredulus pospolitus. Jakoś nie mogę się w tym połapać. Coś mi nie pasuje w tych obliczeniach.
Skoro mamy dane pole dużego trójkąta (na wcześniejszym rsunku zaznaczony na czerwono), to co
| | (4a)2 √3 | |
zostało obliczone? I skąd berze się |
| ? Wzór na pole trójkąta równobocznego |
| | √4 | |
to
Albo podstawiam do wzoru inne dane albo coś gubię po drodze.
30 mar 21:16
a7: ponieważ widzę, że nikt długo nie odpowiada, a Wredulusa chyba teraz nie ma to zwróć uwagę, że
coś źle przepisałeś/zobaczyłeś
Wredulus napisal wzór na pole trójkąta równobocznego o boku 4a poprawnie, następnie podstawił
do tego wzoru dane w zadaniu 18 dm3 i wyliczył bok równy 4a wyszło mu, że będzie on mniejszy
niż 6 czyli na pewno zmieści się w arkuszu (kwadratowym) o boku 9
30 mar 21:41
jezowj : A7, masz rację. Próbowałem znaleźć jakiś punkt zaczepienia.
Dziękuję Wam bardzo Wredulus i a7 za wyjaśnienia i poświęcony czas.
30 mar 22:57