zadanka Mateuszz: 1 Uzasadnij, że liczba 3³² – 1 jest podzielna przez 128. 2 W loterii jest n losów, w tym k (k < n) wygrywających. Jeden los kupuje najpierw osoba A, a później jeden los kupuje osoba B. Która z nich ma większe szanse nabycia losu wygrywającego ? 3 Podaj wzór ogólny na n – ty wyraz ciągu arytmetycznego, którego wszystkie wyrazy są liczbami naturalnymi dającymi przy dzieleniu przez 5 resztę 1, a przy dzieleniu przez 7 resztę 3. 4Znajdź współrzędne punktu przecięcia stycznych do krzywej o równaniu y = x³ + + 2x² – 4x – 3 poprowadzonych w punktach A = (− 2; 5) i B = (0; − 3). Wyznacz wszystkie wartości parametru m, dla których równanie mx² + (m + 3)x + 4 = 0 ma dwa różne miejsca zerowe takie, że suma odwrotności ich kwadratów jest liczbą mniejszą od (m³+7m²)/16 obliczylem dziedzine napisalem wzory vietea podstawilem i nie chce wyjsc

Eta: Za mało tych zadań wrzuć jeszcze z rozmachu w jednym poście następnych 20

ABC: taki dziwny ten zestaw to jakieś kółko matematyczne?

Eta:

Eta: Pewnie jakaś poprawka na dopuszczenie do matury

ABC: Zad 3 można ułożyć równanie diofantyczne: 5x+1=7y+3 5x−7y=2 odgadujemy rozwiązanie szczególne x=6, y=4 stąd wszystkie rozwiązania mają postać x=6+7t y=4+5t gdzie t całkowite więc szukane liczby są postaci 5(6+7t)+1=35t+31 czy też 7(4+5t)+3=35t+31 t≥0 bo chcemy naturalne ciąg 31,66, 101,...

wredulus_pospolitus: I oczywiście ... poza dodaniem zadań to się nawet słowem nie odezwie ... tylko dawać gotowca i nie narzekać

ABC: mnie to tylko ciekawi co to są za zestawy, ten drugi zestaw mi zaburzył koncepcję że to jakaś studencka algebra z teorią liczb bo się styczne pojawiły chyba jednak jakieś ambitne na szóstkę z liceum i chce mieć chłopak za darmo celujący

Mateuszz: To przygotowanie pod maturę, a nie odezwał się bo go nie było

ABC: no to ci powiem że jakaś nietypowa ta matura

Mateuszz: No właśnie poza zadaniem z trójmianu który już mi wyszedł to reszta czarna magia

an: (3¹⁶+1)(3¹⁶−1) itd

ABC: mistrz zwięzłości Mateusz ,an chciał ci powiedzieć że 3³²−1=8 (3²+1)(3⁴+1)(3⁸+1)(3¹⁶+1) i każdy z nawiasów jako liczba parzysta dzieli się przez 2

an: a_n=31+(n−1)*35

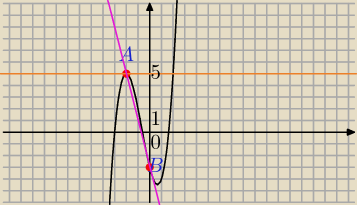
Mila: zadanie 4 y = x³ + 2x² – 4x – 3 f(−2)=−8+8+8−3=5, A=(−2,5)∊krzywej f(0)=−3, B=(0,−3) ∊krzywej Styczne : y=f'(x₀)*(x−x₀)+f(x₀) f'(x)=3x²+4x−4 f'(−2)=0 s₁: y=f'(−2)*(x+2)+5⇔y=5 f'(0)=−4 s₂: y=f'(0)*(x−0)+(−3) y=−4x−3 −4x−3=5 −4x=8 x=−2, y=5 (−2,5) punkt przecięcia stycznych

ABC: A zadanie drugie zrób sam, proponuję zacznij od przypadków najprostszych typu : w loterii są 2 losy w tym jeden wygrywający to zauważysz coś