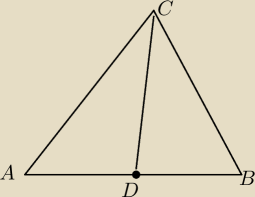
 udowodnil ze odcinek laczacy wierzcholek trojkata z dowolnym punktem lezacym na przeciwleglym
boku (nie bedacym wierzcholkiem)
jest krotszy od co najmniej jednego z pozostalych bokow
No i mam ze
CD<DB+BC
CD<AD+AC
2CD<AB+BC+AC
CD<U{AB+BC+AC}{2]
i cos mi nie wyszlo bo wyszlo ze jest mniejszy od polowy obwodu
udowodnil ze odcinek laczacy wierzcholek trojkata z dowolnym punktem lezacym na przeciwleglym
boku (nie bedacym wierzcholkiem)
jest krotszy od co najmniej jednego z pozostalych bokow
No i mam ze
CD<DB+BC
CD<AD+AC
2CD<AB+BC+AC
CD<U{AB+BC+AC}{2]
i cos mi nie wyszlo bo wyszlo ze jest mniejszy od polowy obwodu
| π | ||
gdzie α ∊(0 ; | ) | |
| 2 |
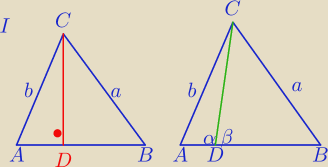 1) CD⊥AB wtedy |CD|<|AC| i |CD|<|BC| jako przyprostokątna w ΔADC i ΔBDC
2) Jeżeli CD nie jest prostopadła do AB, to jeden z kątów : α albo β jest rozwarty
Na rysunku 90<α<180 to CD<b,
α− największy kąt w ΔADC to b jest najdłuższym bokiem w tym Δ⇔CD<b
1) CD⊥AB wtedy |CD|<|AC| i |CD|<|BC| jako przyprostokątna w ΔADC i ΔBDC
2) Jeżeli CD nie jest prostopadła do AB, to jeden z kątów : α albo β jest rozwarty
Na rysunku 90<α<180 to CD<b,
α− największy kąt w ΔADC to b jest najdłuższym bokiem w tym Δ⇔CD<b
 A ja to robilem z nierownosci trojkata . dziekuje
A ja to robilem z nierownosci trojkata . dziekuje