Prosta i punkty 6latek: Na danej prostej wyznacz taki punkt by suma odleglosci tego punktu od dwoch danych punktow byla najmniejsza Bedzie to srodek odcinka A B Tylko teraz nie wiem czy z tresci nie wynika ze te punkty A i B nie leza na tej prostej ?

Pytający: Nie tylko środek odcinka, ale każdy punkt, który leży na odcinku AB ma tę własność

wredulus_pospolitus: Punkt P jest pomiędzy A i B wtedy |AP| + |PB| = |AB| i jest stała, bez względu na położenie punktu P

6latek: Witam no tak . dzieki

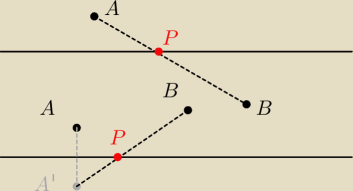
wredulus_pospolitus: Przypadki gdy A,B nie leżą na prostej ( (a) po przeciwnych strona prostej, (b) po tej samej stronie)

6latek: dziekuje Ci

wredulus_pospolitus: Jeszcze został Ci jeden przypadek −−− gdy jeden punkt leży na prostej, a drugi nie

6latek: A to juz za duzo szczesia na raz Tak mowie nie raz do sprzedawczyni jak cos kupuje a ona mi sie pyta co jeszcze Ja wtedy starczy byloby za duzo szczescia na raz

wredulus_pospolitus: Akurat nie ... bo ten ostatni przypadek jest prosty jak się chwilę zastanowisz ... najkrótszą drogą z punktu A (który jest na prostej) do B (który nie jest na prostej) będzie linia prosta ... więc droga |AP| + |PB| > |AB| (gdzie P na prostej), więc 'im szybciej' (im bliżej) idąc od A dotrzemy do tego punktu P i zaczniemy iść bezpośredni w stronę B to tym lepiej (i tym bliżej |AP| + |PB| będzie wartości |AB|)

wredulus_pospolitus: tak wiem ... mało matematyczne wyjaśnienie

wredulus_pospolitus: można (na pewno nie wprost) wykazać, że dla takiego przypadku będziemy mieli P = A

wredulus_pospolitus: i posługiwać się tutaj będziemy nierównością trójkąta