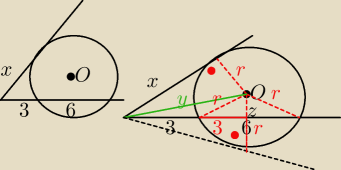
planimetria salv: Oblicz x. Jak narazie tyle wymyśliłem,co na drugim rysunku i poniżej r²+x²=y² r²+x²=36 czyli y=6 z²+36=36 no i wychodzą bzdury,więc coś popsułem

salv: Dobra,skorzystalem z twierdzenia o stycznej i siecznej,ale jak zrobic to bez tego?

wredulus_pospolitus: skąd masz: r² + x² = 36 skorzystaj z: https://matematykaszkolna.pl/strona/4004.html

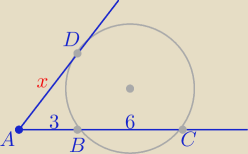
Eta: Z tw. o stycznej i siecznej |AD|²= |AB|*AC| x²=3*9 ⇒ x=....................

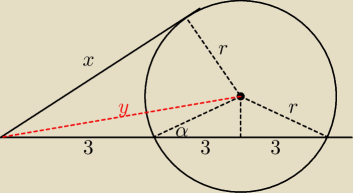
wredulus_pospolitus: z tw. Pitagorasa: y² = x² + r² −> x² = y² − r² z tw. cosinusów: y² = 3² + r² − 2*3r*cos(180−α) = 3² + r² + 6r*cosα z trygonometrii:

	3
natomiast cos α =
	r

więc: y² = 9 + r² + 18 = 27 + r² więc: x² = 27 + r² − r² = 27 −> x = 3√3 i szukaj błędu w moim rozwiązaniu

wredulus_pospolitus: albo i nie

wredulus_pospolitus: to tak jakbyś chciał bez korzystania z tw. o siecznej i stycznej.

salv: Dziękuje za pomoc.A poprowadziłem styczną drugą tą czarną przerywaną i chyba też ma długość x,bo to przecież koło wpisane w kąt i z przystawania trojkątów,ale chyba coś źle,skoro nie wychodzi chyba te 'r' padajace pod katem prostym do stycznej nie dzieli cieciwy na pół,więc tam pewnie nie będzie 6

salv: okrag wpisany w kat*

an: z Pitagorasa z²+6²=y² z²+3²=r² =========== 27=y²−r² x²=y²−r² ========== x=3√3