Osie symetrii 6latek: Wyznacz wszystkie osie symetrii figury zlozonej z a) dwoch okregow b) prostej i okregu c) dwoch prostych Dwa okregi a) rozlaczne b) styczne zewnerznie c) przecinajace sie d) styczne wewnetrznie e) wspolsrodkowe Do przypadku a ) b) c) nalezaloby rozpatrzyc gdy promienie tych okregow sa rowne i rozne do przypadku d) jedna os symetrii przechodzaca przez srodki tych okregow do przypadku e) nieskonczenie wiele osi symetrii Teraz prosta i okrag Prosta prostopadla do prostej przechodzaca przez srodek okregu (czyli jedna os symetrii Dwie proste a) rownolegle (os symetrii to prosta rownolegla do nich i przechodzaca w polowie odleglosci miedzy nimi b) przecinajace sie dwusieczna katow utworzonych przez te proste

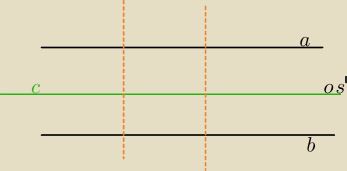
Mila: a||b c− jedna z osi symetrii, i każda prostopadła − czyli nieskończenie wiele osi symetrii

Mila: Oś symetrii figury to taka prosta, że jeżeli złożysz rysunek wzdłuż tej prostej, to obie części się pokryją. ( praktyczne podejście)

6latek: No tak . Faktycznie o tym nie pomyslaem