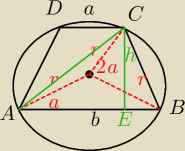
 W okrąg wpisano trapez o wysokości h.Kąt miedzy promieniami okręgu poprowadzonymi do końców
jednego z ramion trapezy jest równy 2α. wykaż, że pole wyraża się wzorem P=h2ctgα.
Czy trapez z tego zadania jest trapezem rownoramienny,ta przyprostokatna powinna sie pokrywac z
2r?A jesli tak,to dlaczego?
W okrąg wpisano trapez o wysokości h.Kąt miedzy promieniami okręgu poprowadzonymi do końców
jednego z ramion trapezy jest równy 2α. wykaż, że pole wyraża się wzorem P=h2ctgα.
Czy trapez z tego zadania jest trapezem rownoramienny,ta przyprostokatna powinna sie pokrywac z
2r?A jesli tak,to dlaczego?
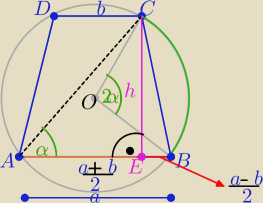 Kąt |BAC|= α −− jako wpisany oparty na łuku BC
trapez jest równoramienny
Kąt |BAC|= α −− jako wpisany oparty na łuku BC
trapez jest równoramienny
| a+b | ||
to |AE|= | ||
| 2 |
| |AE| | a+b | |||
w ΔAEC : ctgα= | ⇒ | =h*ctgα | ||
| h | 2 |
| a+b | ||
P= | *h | |
| 2 |