ostrosłup kasia: Wysokość H prawidłowego ostrosłupa sześciokątnego jest dwa razy większa niż długość a krawędzi jego podstawy. Oblicz cosinus kąta zawartego między sąsiednimi ścianami bocznymi tego ostrosłupa

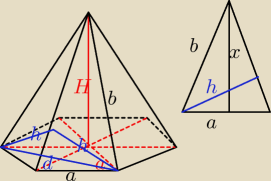
Basia: H = 2a b² = a²+(2a)² = 5a² b=a√5 P=a*x P=b*h x²+(^a₂)² = b²

	a2
x2 +		= 5a2
	4

	20a2−a2
x2 =
	4

	19a2
x2 =
	4

	a√19
x =
	2

	a2√19
P=
	2

P=a√5*h

	a2√19
a√5h =
	2

	a√19
h =
	2√5

d² = a²+a²−2a*a*cos120 d² = 2a²(1+¹₂) = 3a² d=a√3 d²=h²+h²−2h*h*cosα 3a² = 2h²(1−cosα)

	19a2
3a2 = 2*		(1−cosα)
	4*5

	19a2
3a2 =		(1−cosα)
	10

	30
1−cosα=
	19

	30		11
cosα=1−		= −
	19		19

o ile nie pomyliłam się w rachunkach

Bogdan:

1

w

α

α

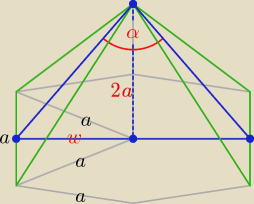
1   a√3 2

√3

w =

a√3,

= tg

⇒ tg

=

=

2

2a

2

2

2a

4

	α   1 − tg2   2		3   1 −   16		13
cosα =		=		=
	α   1 + tg2   2		3   1 +   16		19

Basia: Bogdanie to miały być sąsiednie ściany, a nie przeciwległe

Bogdan: Dziękuję Basiu, źle odczytałem treść zadania.

Basia: Jak udały się ferie ?

Bogdan: Dziękuję, udały się, ale za szybko się skończyły. Zaglądałem chwilami na forum, ale lenistwo mną zawładnęło i nie chciało mi się pisać

Basia: Za to teraz jesteś wypoczęty i pełny chęci do pracy. Przeczytaj post do Ety, Asa i b. Też tam powinieneś być wymieniony, ale nie wiedziałam, że już jesteś

meg: Basiu, mi pole ściany bocznej wyszło √19a²/4 a nie przez 2 nie rozumiem tego właśnie od tego momentu