Tempo zmian funkcji (pochodne) Maths_looser: Dana jest funkcja f(x) = e^x − x. Zbadaj tempo zmian tej funkcji i na tej podstawie wskaż poprawne odpowiedzi. a) funkcja f maleje coraz wolniej dla x ∊ (−∞,0) b) funkcja f rośnie coraz wolniej dla x ∊ (0,∞) c) funkcja f rośnie coraz szybciej dla x∊ (0,∞) d) funkcja f maleje coraz wolniej dla x∊ (0, +∞)

wredulus_pospolitus: no to policz pochodną ... tak ciężko to zrobić

Maths_looser: Gdyby było łatwo to bym pewnie tu nie przychodził po pomoc. Potrzebuje poprawne odpowiedzi w zasadzie na już, a potem będę siedział do rana, aby to zrozumieć...

Maths_looser: Ktoś pomoże?

wredulus_pospolitus: pierdzielę ... człowieku ... jak nie wiesz ile wynosi pochodna z e^x to niby co chcesz przez noc zrozumieć Siadaj na dupie i licz pochodne ... po 2 godzinach już bez większego problemu będziesz liczył pochodnej i dzięki temu także takie zadania nie będą stanowić większego problemu

Maths_looser: pochodna z e^x to oczywiście e^x

Maths_looser: Tutaj trzeba zastosować wzór na pochodne różnicy? Jeżeli tak to e^x−x = −1 + e^x, prawda?

wredulus_pospolitus: f(x) = e^x − x to f'(x) = e^x − 1 (skąd mamy ... f'(x) > 0 −> x > 0 ... więc f(x) rosnąca dla x>0 a malejąca dla x<0 ... odp (d) odpada) teraz liczymy f''(x) = e^x zauważ, że f''(x) >0 dla dowolnego x∊R ... czyli funkcja f(x) jest wypukła,: (górny lewy wykres: http://matematykadlastudenta.pl/strona/259.html) co oznacza, że 'wraz z upływem czasu' rośnie coraz szybciej, a maleje coraz wolniej) Stąd odpowiedzi (a) i (c)

Maths_looser: Okay, a więc.. f ' (x) = e^x − 1 f ' (x) > 0, a więc e^x−1 > 0 <=> e^x > 1, tak ?

wredulus_pospolitus: Przykładem funkcji wypukłej która zapewne kojarzysz jest g(x) = x²

wredulus_pospolitus: tak ... e^x > 1 ⇔ e^x > e⁰ ⇔ x > 0

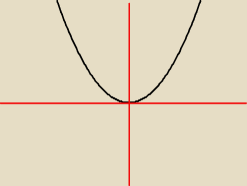
Maths_looser: Tak?

wredulus_pospolitus: tak i jak widzisz ... jak lecimy od lewej i zbliżamy się do x=0 to funkcja 'coraz wolniej maleje' w x=0 mamy ekstremum i później im bardziej się od niego oddalamy tym szybciej funkcja rośnie

wredulus_pospolitus: analogicznie będzie dla f(x) = e^x−x (chociaż sam wykres wygląda z goła inaczej

Maths_looser: skoro f ' (x) = e^x −1 to zgadzam się definitywnie, iż f '' (x) = e^x, a skoro tak to e^x>0, idąc dalej tym tropem zgadzam się iż jeżeli podstawimy pod "x" dowolną rzeczywistą to na pewno e^x>0

wredulus_pospolitus: ok ... jeśli ogarnięte, to podbijaj następne

Maths_looser: Nie wiem czy dobrze rozumiem, ale żeby obliczyć tempo zmian to muszę w zasadzie policzyć f ' (x), odczytać jak się to zachowuje/jak wygląda na wykresie, następnie policzyć f '' (x), aby mieć dalszy kawałek wykresu, znów to sobie przedstawić na wykresie, a potem wychodzi dzięki temu funkcja chociażby g(x)=x² i dzięki niej możemy dojść do tego gdzie rośnie gdzie maleje, gdzie szybciej gdzie wolniej?

wredulus_pospolitus: tak ... aczkolwiek w sobotę postaram Ci się podać pewne 'drogi na skróty' które mogą Ci szybciej 'wydedukować' jaką będziesz miał sytuację

Maths_looser: Wow, już dziś jestem Ci niesamowicie wdzięczny. Czy mógłbym Ci się jakoś zrekompensować? Podziwiam samo to, że chcesz swój cenny, prywatny czas poświęcać na rozwiązywanie moich zadań, a co dopiero jeszcze uczyć mnie tego tematu...

wredulus_pospolitus: Szykuję się do zakupu używanego auta dla mamy ... możesz zafundować Bez obaw − cena będzie w okolicach 10 tys. Euro

Maths_looser: Hmm.. Obawiam się, że nie poratowałbym Cię w tej chwili nawet w PLN, a w Euro byłoby już to na pewno nie możliwe

Maths_looser: W zasadzie 1 test na 3 rozwiązany, dzięki temu, iż ten pierwszy jest 10/10 pkt. to w zasadzie nie musze robić pozostałych dwóch podejść. Natomiast dobrze by było mieć odpowiedzi chociaż to potem ucząc się do egzaminu obliczałbym sobie sam, ale chociaż miałbym już poprawne odpowiedzi, więc mógłbym zweryfikować czy dobrze zrobiłem. Jak chcesz to mogę wstawić zadania, chociaż już bardzo późno, nie chce Cię wykorzystywać już tak bardzo

Maths_looser: Inaczej, zaznaczę wszystkie odpowiedzi i system sam pokaże, które prawidłowe. Nie będę Cię prosił, abyś mi pozostałe 5 zadań rozwiązał z kolejnych dwóch podejść, a więc 10 łącznie, bo bym Cię do rana tutaj denerwował

Maths_looser: Jak mógłbym Cię zlokalizować tutaj, abyś podesłał mi jakiś "kurs", nie ukrywam, iż to dla mnie dość ważne, na pewno wiele by mi to pomogło

wredulus_pospolitus: albo daj linka do strony ... będziesz szybciej niż wstawiać pojedyncze zadania

Maths_looser: To jest system, mogę co najwyżej screeny podesłać Ci tutaj.

wredulus_pospolitus: A co do pochodnych − http://staff.uz.zgora.pl/jskowron/pliki/MPT3.pdf moje dawne 'podstawowe' źródło przykładów. Same pochodne zaczynają się od 99 strony.

wredulus_pospolitus: chociaż jak teraz patrzę na te pochodne to mogą być one trochę za trudne dla Ciebie (ale link zachowaj ... tutaj będziesz miał sporo różnej maści całek)

Maths_looser: Jak cokolwiek będziesz miał to umówmy się, że tutaj mi je wstawiaj (linki) etc. Ja sobie zapiszę to stronę.

wredulus_pospolitus: To wrzucaj screeny do tego tematu (nie ma potrzeby kolejnego tworzyć) ... to się raz dwa to zrobi

Maths_looser: 1...…. https://zapodaj.net/7aed5a56101b3.png.html

Maths_looser: 2...…… https://zapodaj.net/7a471c400cc5c.png.html

Maths_looser: 3...……. https://zapodaj.net/86c5f62108b01.png.html

Maths_looser: 4...……. https://zapodaj.net/73a8e413ecaba.png.html

Maths_looser: Po rozwiązaniu tych 4 mogę otworzyć nowe podejście. Podesłałem 4, gdyż piąte się powtórzyło.

wredulus_pospolitus: 1.

	1
f(x) =		e2x
	x

	1		1		1		1
f'(x) = (		)'e2x +		*(e2x)' = −		e2x +		*2e2x =
	x		x		x2		x

	2x − 1		e2x		1
= e2x(		) =		( 2 −		)
	x2		x		x

więc odp (a), (b) i (c) są poprawne

wredulus_pospolitus: 2) f(x) = x*e^x f'(x) = (x)'e^x + x*(e^x)' = 1*e^x + x*e^x = e^x(1+x) więc f''(x) = ( e^x*(x+1) )' = e^x*(x+1) + e^x*1 = e^x(x+2) f'''(x) = (e^x(x+2))' = e^x(x+2) + e^x*1 = e^x(x+3) więc odp b i c

wredulus_pospolitus: f(x) = x⁴ + 6x to: f'(x) = 4x³ + 6 f''(x) = 12x² więc odpowiedzi (b) i (d) odpadają zauważ, że f''(x) ≥ dla dowolnego x∊R (pominę fakt, że mówimy o wypukłości tylko gdy f''(x) > 0 ) w takim razie funkcja f(x) jest wypukła w x∊R Odp c

wredulus_pospolitus: zad 4 już było tutaj podawane

wredulus_pospolitus: aj nie ... dobra f(x) = e^x + x no to: f'(x) = e^x + 1 (zauważ, że f'(x) > 0 dla dowolnego x ... więc funkcja zawsze rośnie, więc odp (a) i (b) odpadają) f''(x) = e^x (zauważ, że f''(x) > 0 dla dowolnego x ... więc f(x) jest wypukła) A co się dzieje z funkcją gdy jest rosnąca i wypukła? 'rośnie coraz szybciej' czyli odp (c)

Maths_looser: Było trochę inne. Trochę inna dana funkcja i trochę inne odpowiedzi

Maths_looser: Dobry jesteś powiem Ci, jesteś profesorem? Czy zakochałeś się w pochodnych?

wredulus_pospolitus: Ani jedno ani drugie − po prostu: 1) nie chodziłem do gimnazjum (stary system) 2) pochodne miałem w liceum 3) na starej maturze było jedną 'typowe' zadanie; "zbadaj przebieg zmienności funkcji" (które wymagało m.in. umiejętność liczenia pochodnych), przygotowując się do matury na zajęciach przerobiłem dziesiątki tych przykładów tak, że robiłem je niemalże w pamięci (patrząc na wzór funkcji już wiedziałem mniej więcej jak będzie wyglądał jej wykres). 4) pochodne to nic strasznego, to zwyczajne podstawianie do gotowych wzorów

Maths_looser: 1.....https://zapodaj.net/48d5b0a13dc02.png.html

Maths_looser: 2 …………. https://zapodaj.net/e430d425fa09a.png.html

Maths_looser: 3...….. https://zapodaj.net/d0dd96c751237.png.html

Maths_looser: 4...…. https://zapodaj.net/2ae92857b75d2.png.html

wredulus_pospolitus: uuu ... całeczki ... no to tutaj wysiądziesz jeżeli nie opanujesz pochodnych

Maths_looser: 5...…… https://zapodaj.net/9a3a7293e7fcc.png.html

Maths_looser: Nie poradzę sobie kompletnie bez znajomości pochodnych? A więc rozumiem, że pochodne to taki konieczny wstęp do całek?

wredulus_pospolitus: 1)

	x3 − 2√x		1
∫		dx = ∫ (x2 − 2		) dx = ∫ x2 dx − ∫ 2x−1/2 dx =
	x		√x

	x3
=		− 4x1/2 + C
	3

więc odp (a) i (b) prawidłowe ... odp (c) także (pochodna z wyniku całki = funkcji pod całką −−− w ten właśnie sposób sprawdza się czy dobrze policzyliśmy całkę ... bo 'liczenie pochodnej jest o wiele łatwiejsze niż całek' ) odp (d) NIE JEST prawidłowa, bo wynikiem całki nieoznaczonej jest cała RODZINA funkcji 'na końcu będzie +C' co oznacza dowolna stałą liczbę tak więc: ∫ 1 dx = x + C bo zarówno (x+1)' = 1 jak i (x+5)' = 1 jak i (x)' = 1 i to własnie reprezentuje to '+C' na końcu

Maths_looser: Woo, tu już wchodzimy powoli do świata magii. Mimo wszystko odpowiedz a,b,c poprawna, odpowiedz D niepoprawna?

wredulus_pospolitus: 2)

	1
ctgx * tgx =		* tgx = 1 (powtórka z trygonometrii )
	tgx

więc ∫ ctgx*tgx dx = ∫ 1 dx = x + C (patrz co napisałem na końcu poprzedniego postu − nie wiedząc że będą później liczył taką całkę) więc mamy odpowiedzi (a) i (c)

Maths_looser: Okay, a więc 1) a,b,c, 2) a,c

Maths_looser: Ty szybciej to rozwiązujesz aniżeli ja czytam jedynie.

wredulus_pospolitus: 3)

	x2ex + 2x		x2ex		2x
∫		dx = ∫		dx + ∫		dx =
	x2		x2		x2

	2		1
= ∫ ex dx + ∫		dx = ∫ex dx + 2∫		dx =
	x		x

= e^x + 2*ln|x| + C więc odpowiedź (a) i (b) prawidłowa odpowiedź (c) NIE JEST prawidłowa,

	2
prawidłowym zapisem byłoby ∫ ( ex +		) dx
	x

zapis bez nawiasu jest nieprawidłowy ... tak jakbyśmy napisali (x+2)² jako x + 2² <chociaż ten zapis ma przynajmniej jakiś sens ... ten w odpowiedzi (c) nie ma żadnego sensu pod względem matematycznym)

wredulus_pospolitus:

	1
a (d) NIE JEST prawidłowa, bo po prostu jest źle policzona ∫		dx ... zamiast policzyć
	x

całkę policzona tam została pochodna.

wredulus_pospolitus: 4)

	ex		ds
∫		dx = // s = ex + 1 ; ds = ex dx // = ∫		= ln|s| + C = ln|ex+1| + C =
	ex+1		s

= ln(e^x + 1) + C odpowiedź (a) jest NIEPRAWIDŁOWA odpowiedź (b) ... a w życiu odpowiedź (c) i (d) są prawidłowe. W celu policzenia tej całki skorzystałem z metody 'podstawienia', jest to jedna z dwóch najpowszechniej używanych metod ułatwiających liczenie całek.

Maths_looser: A coś kojarzę podstawienie i przeliczenie.

wredulus_pospolitus: 5)

	1
tutaj przydaje się wiedza o pochodnych, otóż (tgx)' =		... dzięki temu wiemy jakie
	cos2x

podstawienie zrobić

	1 + 2tgx		2		ds		1
∫		dx = // s = (1 +2tgx) ; ds =		dx ⇔		=		dx
	cos2x		cos2x		2		cos2x

// =

	s		1		1
= ∫		ds =		s2 + C =		(1+2tgx)2 + C
	2		4		4

więc odpowiedzi (c) i (d) są prawidłowe

wredulus_pospolitus: nie przeliczanie tylko 'przez części'

Maths_looser: Zgadza się, to akurat świeci mi się gdzieś na końcu głowy. Powiem Ci, że jesteś niesamowicie dobry w te klocki.. Jak byś chciał to mam ostatnie 5 zadań. Aczkolwiek, aż głupio mi pytać.

Maths_looser: Dałeś mi tyle tutaj dobrego od siebie, że jestem moralnie zobligowany do tego, aby to wszystko przyswoić i posiąść wiedzę, której brakuje..

wredulus_pospolitus: Dajesz ... ale pamiętaj że w sobotę siadasz i 'ogarniasz' pochodne ... później jeszcze będzie Ciebie czekała 'zabawa' z całkami

Maths_looser: Zrobię to, bo moralność mi inaczej nie pozwoli. Chociażby z szacunku do tego ile dobra tutaj wylałeś i ile czasu poświęciłeś to muszę to zrobić, posiąść tą wiedzę.

wredulus_pospolitus: zostało 14 min.

Maths_looser: 1..... https://zapodaj.net/9f6f80add1a0a.png.html

Maths_looser: 2 ………. https://zapodaj.net/f2db9ab23823f.png.html

Maths_looser: 3...……. https://zapodaj.net/d2ebcb3bb8ab1.png.html

Maths_looser: 4...…… https://zapodaj.net/1bfdef473ea6d.png.html

Maths_looser: 5 …………. https://zapodaj.net/5aa2a0247b4fd.png.html

Maths_looser: Jak to rozwiążesz to powiem Ci, że jesteś dla mnie Królem i mistrzem w jednym. +jeżeli takich rzeczy dawniej uczyli i po tylu latach (zapewne) to wszystko pamiętasz to aż mi wstyd za siebie i dzisiejsze nauczanie.

wredulus_pospolitus: 1)

	x4
∫ (x3 − 3x2 + 4x −7) dx =		− x3 + 2x2 − 7x + C
	4

więc 2

	x4
∫ f(x) = [		− x3 + 2x2 − 7x]21 =
	4

1

	24		14
=		− 23 + 2*(2)2 − 7*2 − (		− 13 + 2*12 − 7*1) =
	4		4

	1		3		1		17
= 4 − 8 + 8 − 14 − (		− 1 + 2 − 7) = −10 − ( −5		) = −4		= −
	4		4		4		4

więc odp (b) także odp (d) jest prawidłowa (cała sumy równa jest sumie całek ... analogicznie do tego co wcześniej robiłem)

wredulus_pospolitus: 2)

	5
f(x) =		− 6x
	x

funkcja pierwotna

	5
F(x) = ∫ f(x) dx = ∫ (		− 6x) dx = 5ln(|x|) − 3x2 + C
	x

F(e) = −3e² ⇔ 5ln|e| − 3e² + C = −3e² ⇔ 5 − 3e² + C = −3e² ⇔ C = −5 więc odp (d) ... dodatkowo odpowiedź (c) jest prawidłowa

wredulus_pospolitus: Czas jest do 00:00

Maths_looser: Postaram się to przeanalizować w weekend, czyli odpowiedz b oraz d prawidłowa?

Maths_looser: Zadanie 1 odpowiedz b,d Zadanie 2 odpowiedz c,d

Maths_looser: Na te wcześniejsze zadania miałem czas do 00:00. Te 5 zadań aktualnych do jutra włącznie.

wredulus_pospolitus: 4) P = 2∫₀^pi/2 cosx dx = 2*(−sinx)|₀^pi/2 = 2*[−sin(pi/2) − (−sin0)] = 2*[ 0 + 1] = 2 więc odp (a) i (d)

wredulus_pospolitus: oki ... to nie musze sie tak spieszyć

Maths_looser: Nie, nie. Powinienem Ci to w zasadzie powiedzieć wcześniej, a Ty w 3/4 minuty rozwiązujesz te zadania i co najlepsze prawidłowo. Nie wiem jak Ty to robisz. Wykładasz może korepetycje swoją drogą?

wredulus_pospolitus: Nie mam cierpliwości do korepetycji, a po drugie − wyżyć z tego się nie da

Maths_looser: Tak myślisz? Nie wiem skąd jesteś, ale załóżmy w Warszawie za h zajęć trzeba 50 zł zapłacić. Załóżmy, że dziennie miałbyś 5 uczniów, a więc dziennie 250 zł na rękę. Oczywiście musiałbyś sobie mini szkołę założyć, aby przyjmować 5 uczniów załóżmy 5 dni w tygodniu, ale znam taką osobę, która to robi.

wredulus_pospolitus: 3) średnią wartość funkcji na przedziale [a,b] obliczamy ze wzoru:

∫ab f(x) dx
b−a

czyli mamy:

	1
średnia wartość =		∫−21(2x2 − x) dx =
	1 − (−2)

	1		x3		x2		1		15		5
=		* [		−		]−21 =		*		=
	3		6		2		3		2		2

więc odp (a) prawidłowa odp. (b) i (d) odpadają na wstępie bo BRAKUJE NAWIASU odp (c) odpada

Maths_looser: Powiem Ci, że siedzę i za każdą Twoją następną odpowiedzią, rozwiązaniem doznaje coraz to głębszego szoku i niedowierzania. Ile musiałeś włożyć w to pracy swego czasu, aby dojść do takiej perfekcji. Nie jeden nauczyciel/wykładowca nie powstydziłby się takich zdolności.

Maths_looser: Poradzisz sobie z tym 5? Bo ja to tonę w samym poleceniu..

wredulus_pospolitus: 5) P'(t) = 4e^−0.08t P(t) = ∫ P'(t) dt = −50e^−0.08t + C odp (a) prawidłowa, tak samo (d) (tutaj jest pokazane podstawienie) ... odpowiedź (c) także prawidłowa (to o ile dobrze pamiętam jest nawet definicją funkcji pierwotnej) Pozostało nam policzyć: P(6) − P(0) = [−50e^−0.08t ]₀⁶ = −50e^−0.48 − (−50) = 19.0608 ≈ 19.061 więc także i odp (c) jest prawidłowa

Maths_looser: Rozumiem, iż odpowiedz A, C, D prawidłowa. Jedynie odpowiedz B błędna?

wredulus_pospolitus: B także prawidłowa

wredulus_pospolitus: źle napisałem na końcu

Maths_looser: Czyli wszystkie 4 odpowiedzi są poprawne?

wredulus_pospolitus: Jeżeli będziesz miał z egzamin z matematyki na koniec semestru to MUSISZ siąść do pochodnych i całek bo się po prostu ośmieszysz na egzaminie.

wredulus_pospolitus: tak

Maths_looser: Okay, a masz jakiś kurs/zadania/informacje/porady/skróty/sposoby/ cokolwiek z całek, pochodnych i ogólnie tego działu?

wredulus_pospolitus: co do całek −−− to podany zbiór zadań masz tam najpierw wyjasnione na przykładach jak liczysz całki poszczególnymi metodami ... później masz szereg całek które po prostu rozwiązujesz. Całki to jest ta część analizy którą po prostu trzeba 'przerobić' w sensie −−− zrobić setki (tak jest SETKI) przykładów. Wierz mi ... jeżeli zrobisz paręset całek to później po pierwszym spojrzeniu na jakąś całkę będziesz instynktownie wiedział jak ją rozwiązać czy też jaki będzie mniej więcej wynik tejże całki. Co do pochodnych − na start materiał na matematyka.pisz.pl ... a tak to bym musiał się zastanowić.

wredulus_pospolitus: PS. Siadanie do całek bez opanowania pochodnych mija się całkowicie z celem.

Maths_looser: W zadaniu 3 oraz 4 zbyt mało poprawnych odpowiedzi, to znaczy te które podałeś są prawidłowe, ale jeszcze jakieś są, których nie zaznaczyliśmy. Wynik 6/10 z jednej strony można powiedzieć, iż jest bardzo zadawalający i jestem bardzo Ci wdzięczny, ale nie chce abyś pomyślał, iż fascynuje mnie wynik 6/10 jako ogólnie, bo tak nie jest. Natomiast w tym przypadku, kiedy mi pomagasz to jestem bardzo zadowolony z niego. Dodam, iż z poprzednich "piątek" zadań wynik 10/10 oraz 8/10, a teraz 6/10, ale to i tak dla mnie bardzo satysfakcjonujący wynik. Sam zrobiłbym maksymalnie każdy z tej "piątki zadań' na 2/10. Bardzo jestem Ci wdzięczny

wredulus_pospolitus:

	1
Jeżeli nie będziesz wiedział że pochodną z lnx jest		to nie będziesz wiedział, że
	x

	1
∫		dx = ln|x| + C.
	x

To jest po prostu niemożliwe.

Maths_looser: Okay, z pewnością wezmę pod uwagę Twoje słowa jak i stronę, którą mi podałeś. Jak zapiszę link tego okna na matematyka.pisz to on nigdy tutaj już nie usunie się, prawda? Oczywiście spadnie w zadaniach pewnie gdzieś daaaaaaaaaleko, ale po linku zawsze go namierzę, nie prawdaż?

wredulus_pospolitus: w 3 tylko (a) jest prawidłową odpowiedzią i gdyby prowadzący stwierdził, że także niby (b) jest prawidłową odpowiedzią to bym go zrównał z ziemia za twierdzenie, że: ∫ 2x² − x dx to prawidłowy zapis

Maths_looser:

	1
Bardzo sensownie wygląda		w przypadku całek względem pochodnych. Widać tu duże
	x

nawiązanie, ale tak znajomość podstaw to klucz do rozszerzeń.

Maths_looser: Mogę reklamować zadanie, myślisz, iż warto?

Maths_looser: W jaki sposób najlepiej wytłumaczyć reklamację?

wredulus_pospolitus: w 4 zaznaczyłeś które odpowiedzi ? a i d I dobrze odpowiedź (b) odpada bo wtedy P = 2*0 − 2*1 = −2 < 0 ... i niech no prowadzący powie, że pole tej figury ma wartość ujemną natomiast skoro już zaznaczyliśmy, że odp (a) i P = 2 ... to przecież nie może być P = 2π więc wybacz, ale nie przyjmuję do wiadomości możliwość taką, że a i d to nie są wszystkie prawidłowe odpowiedzi

wredulus_pospolitus: w powyższy sposób możesz zareklamować (4) zadanie ... tylko przestudiuj w jaki sposób wyliczona zostało 'P'

wredulus_pospolitus: a pamiętasz które z poprzedniej listy było 'niepełne'

Maths_looser: Zgadza się w zadaniu nr 4 odpowiedzi A i D

wredulus_pospolitus: To w którym takim razie nie było wszystkich odpowiedzi ?

Maths_looser: Zadanie 4 zareklamowane. Zadanie 3 jeszcze było niepełne. Zaznaczyłem odpowiedz A ona jest prawidłowa, lecz brakuje czegoś.

wredulus_pospolitus: to reklamujesz zadanie 3. Uzasadnienie.

	∫ab f(x) dx
'Korzystamy ze wzoru wartość średnia =		'
	b − a

Związku z tym D jest nieprawidłowa.

	1
zapis		∫−21 2x2 − x dx jest nieprawidłowy ... powinno być:
	3

1		1
	∫−21 (2x2 − x) dx lub		( ∫−21 2x2 dx − ∫−21 x dx) z tego powodu
3		3

odpowiedź (B) odpada Odpowiedź (C) odpada ponieważ wyszła nam (A) prawidłowa − a te dwie odpowiedzi się wzajemnie wykluczają −−− prowadzący NIEPRAWIDŁOWO traktuje odpowiedź (b) jako poprawną.

wredulus_pospolitus: a z poprzedniej listy także zapewne zadanie (3) było 'niepełne' ... jeżeli tak to dokładnie z tego samego powodu co tutaj (na tamtej liście w zadaniu 3 zapewne odpowiedź (c) traktował jako prawidłową).

Maths_looser: Ok, taką reklamację przedstawię.

wredulus_pospolitus: Czy to są zadania od prowadzącego ćwiczenia czy prowadzącego przedmiot?

Maths_looser: Wykłady i ćwiczenia.

Maths_looser: Reklamacja swoją drogą wysłana. Do tej poprzedniej "piątki" nie mogę niestety już złożyć reklamacji, gdyż zamknąłem "okienko"

wredulus_pospolitus: To pójdź do niego na konsultacje i z tym zadaniem i zapytaj się dlaczego było niepełne.

Maths_looser: Ok, tak też zrobię mimo iż wysłałem reklamację, na którą muszę otrzymać odpowiedz. Nie wiem jak Ci dziękować. Bez Ciebie nigdy bym tego nie zrobił. Jestem Ci wdzięczny jak chyba nigdy nikomu. Jakbyś coś miał z pochodnych/całek to podeślij tutaj, będę Ci bardzo wdzięczny, z pewnością się przyda, bo moje zobowiązanie to nie tylko słowa, a ciężka praca z tematem.

Jerzy:

	ex + e−x
∫		dx
	ex − e−x