Ostroslup prawidlowy trojkatny. Wyznacz cosinus Masny: Krawędź podstawy ostrosłupa prawidłowego trójkątnego ma długość 6 a krawędź boczna jest równa 4. Oblicz cosinus tego ostroslupa.

Eta: Popraw treść pytania do zadania

Masny: Kurcze nie pamietam dokladnie Bylo cos zeby Obliczyc cosinus tego ostroslupa do plaszczyzny Jego podstawy.

ZADANIE: up.

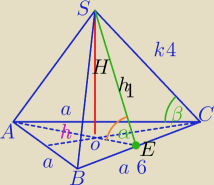Mila: 1) β− kąt między krawędzią boczną a płaszczyzną podstawy 2) α− kąt między ścianą boczną a płaszczyzną podstawy 3) kąt między ścianami bocznymi ( w drugim wątku będzie) Ad1) a) W ΔABC:

	a√3		6√3
h=		=		, h=3√3
	2		2

	2		1
|OC|=		h=2√3, |OE|=		h=√3
	3		3

b) W ΔSOC:

	|OC|		2√3
cosβ=		⇔cosβ=		,
	k		4

	√3
cosβ=		− cosinus kąta między krawędzią boczną a płaszczyzną podstawy
	2

===================================================== 2)W ΔSEC:

	1
k2=h12+(		a)2⇔42=h12+32
	2

h_b¹=16−9=7, h₁=√7

	|OE|
cosα=		⇔cosα=U{√3}{√7
	h1

	√21
cosα=		−cosinus kąta między ścianą boczną a płaszczyzną podstawy
	7

===================================================

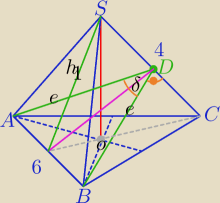Mila: 3) kąt między ścianami bocznymi BD⊥SC, AD⊥SC, |AD|=BD| a) h₁=√7

	1
PΔBCS=PΔABS=		*6*√7=3√7
	2

	1
PΔBCS=		*4*e
	2

	3√7
2e=3√7⇔ e=
	2

b) W ΔBDA z tw. cosinusów: |AB|²=e²+e²−2e*e*cosδ 6²=2*e²*(1−cosδ)

	3√7
36=2*(		)2*(1−cosδ)
	2

	9*7		4
18=		*(1−cosδ) /*
	4		9*7

	4
1−cosδ=18*
	9*7

	8		8
1−cosδ=		, 1−		=cosδ
	7		7

	1
cosδ=−		− cosinus kąta między ścianami bocznymi (kąt rozwarty)
	7

================================= posprawdzaj rachunki.