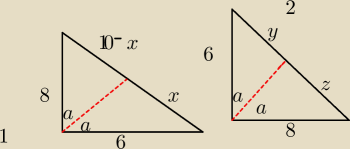
planimetria asd: W trojkacie prostokatnym poprowadzono dwusieczna kata prostego.Oblicz dlugosc odcinka wycietego z tej dwusiecznej przez brzeg trojkata,wiedzac,ze przyprostokatne maja dlugosci 8 i 6. No i wiadomo przeciwprostokatna ma liczac z pitaograsa 10.Po lewej jest moj rysunek,po prawej jest z ksiazki. Ja zrobilem ten w ten sposob ( z twierdzenia o dwusiecznej)

10−x		8
	=
x		6

	30
i x wychodzi
	7

no i pomijajac tam dalsze obliczenia ktore daja dlugosc

	z		8		40
W rozwiazaniu ksiazkowym natomiast zrobili y+z=10,		=		,wychodzi z=		.Co jest
	y		6		7

blednego w moim rozwiazaniu? I skad mam wiedziec ktora przyprostokatna ma 8,ktora 6?Bo jezeli

	10−x		6
zrobie w ten sposob proporcje u mnie		=		,to wychodzi tak jak w rozwiazaniu
	x		8

ksiazkowym.

iteRacj@:

30		40
	+		=10
		7

po prostu raz zostaje wyliczony krótszy odcinek, raz dłuższy

iteRacj@:

30		40
	+		=10
7		7

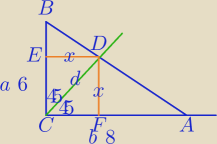Mila: Nic nie ma błędnego.

	30		40
10−		=		=z
	7		7

Patrz jak układasz proporcję : z jest "sąsiedni" do dłuższej przyprostokątnej, w Twoim rysunku z lewej obliczyłeś dł. odcinka x sąsiedniego do krótszej przyprostokątnej Inny sposób: ΔBED∼ΔBCD⇔

|BE|		6
	=
|ED|		8

6−x		6
	=
x		8

6x=8*(6−x) 6x=48−8x 14x=48

	48		24
x=		, x=
	14		7

	24√2
d=
	7

Ogólnie wzór na dł. odcinka dwusiecznej"

	a*b√2
d=
	a+b

=========== II sposób

	1
PΔABC=		*6*8=24
	2

Lub suma pól:

	1		1		√2		√2
PΔABC=		*6*d*sin45+		*d*8 *sin45=3d*		+4d*
	2		2		2		2

7√2
	d=24
2

	2
d=24*		⇔
	7√2

	24√2
d=
	7

===========

asd: glupi jestem,dzieki za pomoc