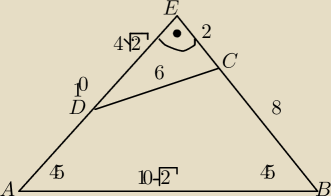
Pole czworokąta ABCD antoni: Oblicz pole czworokąta ABCD, w którym |AB|=10√2, |BC|=8, |CD|=6 oraz ∡ABC = ∡BAD = 45 stopni.

a7: P_A−B_CD=PΔ_ABC−PΔ_DCE=50−4√2

a7: poprawka

	10*10		4√2*2
PABCD=PΔABE−PΔDCE=		−		=50−4√2
	2		2

a7: 1.przedłużamy boki BC i AD i otrzymujemy trojkąt prostokątny równoramienny ABE, więc |AE|=|BE|=10 skoro |AB|=10√2 oraz |EC|=10−8=2, |DE| liczymy z tw.Pitagorasa 2. zauważamy że szukane pole czworokąta to pole ΔABE odjąć pole ΔDCE 3. robimy obliczenia

antoni: ahh no tak, wystarczylo sobie trojkacik dorysowac i wszystko jasne. dziękuje bardzo a7

a7: