przebieg zmiennosci student: f(x)=³√x²−1 Pochodna nie jest określona dla 0 (ponieważ mianownik by się zerował), a w odp. podane jest, iż tam jest minimum (dlaczego? 1)pytanie.). Plus druga pochodna będzie ujemna, dla wszystkich liczb, oprócz 0 (tak ona również nie jest określona). Jednak wyliczone granice, pochodne i miejsca szczególne wskazywałyby na funkcję podobną do paraboli, a więc wypukłą. Tutaj z drugiej pochodnej wynika, iż to funkcja wklęsła. (2)pytanie)

Jerzy: A gdzie tu masz mianownik ?

student: W pochodnej pojawi się. f'(x)= 2/3 * 1/³√x Więc z dziedziny pochodnej trzeba wyrzucić x=0. Podobnie w przypadku drugiej pochodnej.

student:

	−2
f''(x)=		* 1/3√x4
	9

x⁴ jest zawsze dodatnie, więc druga pochodna jest ujemna wszędzie oprócz zera. A więc funkcja wklęsła. A wydaje się, że powinna być wypukła.

student: Byłabym wdzięczna za pomoc, bo kompletnie już zgłupiałam.

Jerzy: A co powiesz o funkcji y = √x ?

student: A o co pytasz?

student: Na pewno, że jest wklęsła. Ale co wtedy z tym minimum? Bo w odp jest, że oni jest w 0, a przecież tam nie ma pochodnej

Jerzy: Funkcja ma minimum tam, gdzie pochodna nie istnieje.

student: Myślałam, że warunkiem koniecznym na istnienie ekstremum jest zerowanie się pochodnej

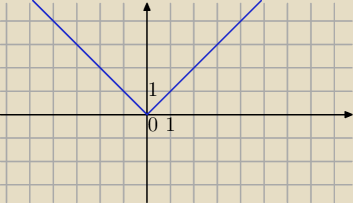
Mila: y=|x| w x=0 nie ma pochodnej, a jest minimum

Jerzy: I dobrze myślałaś,ale to tylko warunek koniezczny,ale nie wystarczający.

Jerzy: Sprawdź funkcję y = x³ . Pochodna się zeruje dla x = 0 , a czy tam jest ekstremum ? Nie, i dlaczego ?