trygonometria, oblicz α jadwigas: naprawde nie rozumiem, bardzo proszę mi wyjaśnić za szczegółami( Punkt P leży na ramieniu końcowym kąta α. Obliczyć sin α,cos α, tg α i ctg α, jeśli : a) p(2,3) b) P(−1,2) c) P(−2,2) d) P(2,−3)

Jerzy: A dokładnie czego nie rozumiesz ?

	y
sinα =		, gdzie y to rzędna punktu P , a r to promień wodzący tego pumktu, czyli
	r

długość odcinka |OP| , gdzie O , to początek ykładu współrzędnych.

Jerzy:

	x
cosα =		( x odcieta punktu P )
	r

	y
tgα =
	x

	x
ctgα =
	y

Mila: No i wyjaśniłabym, ale Jadwiga nie pisze czego nie rozumie

PW: Ja wiem. Nie rozumie definicji.

jadwigas: nie rozumiem jak to wygląda na rysunku , i dlaczego wykorzystujecie x, y ,r / nas uczono że to np. Sin a = a przez c

Jerzy: To tylko kwestia oznaczeń.

jadwigas: tylko zaczęłam uczyć się tego więc niczego nie znam

jadwigas: a czy mógł by mi pan wyjaśnić to na rysunku?

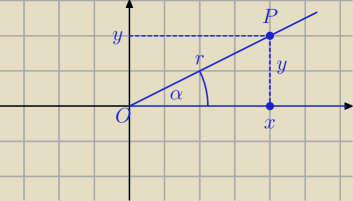
janek191: P = ( x, y) r = I OP I = √x² + y² więc

	y
sin α =
	r

	x
cos α =
	r

	y
tg α =
	x

	x
ctg α =
	y

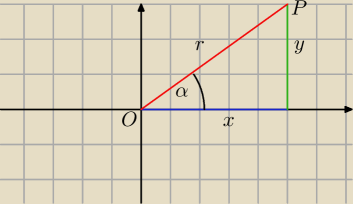
San Tropes: x=5 y=4 r= √x²+y²

janek191: Np. a) P = ( 2, 3) więc x = 2 y = 3 r = √2² + 3² = √13

	y		3		3 √13
sin α =		=		=
	r		√13		13

	x		2		2 √13
cos α =		=		=
	r		√13		13

	y		3
tg α =		=
	x		2

	x		2
ctg α =		=
	y		3

jadwigas: dziękuję bardzo =))))

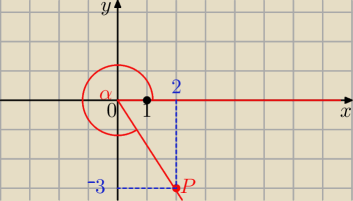
janek191: d) P = ( 2, − 3) x = 2 y = − 3 r = √2² + ( − 3)² = √4 + 9 = √13

	y		− 3		3√13
sin α =		=		= −
	r		√13		13

	x		2		2√13
cos α =		=		=
	r		√13		13

	y		−3		3
tg α =		=		= −
	x		2		2

	x		2		2
ctg α =		=		= −
	y		−3		3