kwadrat matura: W kwadracie ABCD punkt E jest środkiem boku AB , a punkt F jest środkiem boku BC Odcinki AF i DE przecinają się w punkcie M Wykaż,że długość |MC|=|AB|

an:

Eta: 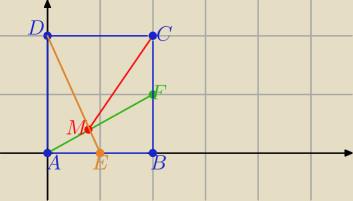2 sposób ( analitycznie) bez straty ogólności przyjmuję bok kwadratu długości 2 i umieszczam go w układzie współrzędnych A(0,0) , B(2,0), C(2,2) , D(0,2) prosta k: y−0,5x prosta p : y= −2x+2 rozwiązując układ równań k∩p={M} M(0,8; 0,4) i C(2,2) to |MC|= ...... = 2= |AB| c.n.w.

Eta: E(1,0) i F(2,1)

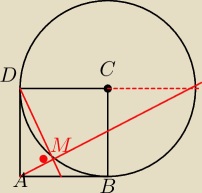
an: Maturzysta analizując rysunek nie powinien mieć problemów z wyciągnięciem p/n wniosków. Trójkąty DAE i AFB są przystające i podobne do DME ⇒∡ DMF jest kątem 90^o prosta przedłużenie AF przecina przedłużenie DC w D' tworząc odcinek równy 2*DC=DD' będący średnicą okręgu, na którym oparty jest kąt prosty DMD'=DMF z tego wynika, że CM=DC jako promienie okręgu.

Eta: Ja nie kwestionuję Twojego dowodu Podałam 2 sposób .........

Eta: Tak dla ścisłości ........DME nie tworzą trójkąta

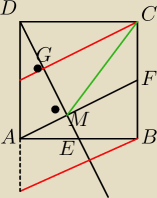
an: 3 sposób Kąt DMA jest prosty wyjaśniam wyżej, DG=GM Tales⇒ czyli trójkąty DGC i CGM o wspólnym boku CG są przystające, a więc CD=CM cnw. Czy istnieje prostsze rozwiązanie ?. Ja na 100% nie wiem. Tak dla ścisłości "....... k: y−0,5x", czy ten zapis opisuje prostą ⇒ no cóż chochliki buszują. Uważam, że ucznia należy zmusić do myślenia, a nie uważając jak często nauczyciele mówią że jest głupi to trzeba zrobić za niego, myśląc na pewno zmądrzeje, a jak nie będzie chciał to jego wybór, pomocnik murarza, kasa w biedronce takich też potrzeba, ale najpierw trzeba mu dać szansę. Czy ja kwestionuję Twoje ? Choć uważam, że nie....m* jest podawanie uczniom gotowych ściąg zwłaszcza przez nauczycieli, choć w tym konkretnym przypadku pozostawiłaś pewien margines dla ucznia. POZDRAWIAM