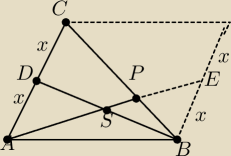
Dowód geo do sprawdzenia Ateusz: Sprawdzenie rozwiązania Dany jest trójkąt ABC , w którym BC = a . Z wierzchołka B poprowadzono środkową BD do boku AC. Punkt S jest środkiem odcinka BD. Przez punkty A i S poprowadzono prostą, która

	2
przecięła bok BC w punkcie P . Wykaż, że długość odcinka CP jest równa		a
	3

Spróbowałem zrobić to tak jak uczyła Mila : (rysunek) ΔAPC ~ ΔBPE

	BE		x		1
k=		=		=
	AC		2x		2

BP		1
	=k=
CP		2

CP=2BP a=CP+BP=3BP

a		3
	=
CP		2

	2
CP=		a cnd.
	3

I teraz pytanie : Czy wszystko jest tutaj w porządku? Bo odbijając izometrycznie trójkąt nie byłem właściwie pewien, czy wszystko prawidłowo robię, np. nie wiem czy AE na pewno przechodzi przez P? Założyłem, że tak, ale nie jestem w stanie tego matematycznie ani geometrycznie udowodnić.

Hajtowy: 3 sposoby rozwiązania: https://www.zadania.info/d1426/4221441

iteRacj@: 1/ ostatnie zdanie: Czy dowód geometryczny nie jest dowodem matematycznym? 2/ odbijając izometrycznie trójkąt ← na czym to polega? 3/ czy AE na pewno przechodzi przez P ← to zależy od tego jak wyznaczony został pkt P? 4/ ΔAPC ~ ΔBPE na podstawie jakich własności? trzeba to wykazać

Ateusz: 1. Jest. Zostawmy to... 2. Odbić symetrycznie względem jednego zboków, izometrycznie czyli zachowując długość boków 3. Tak jak w poleceniu, jest to punkt wspólny przedłużonej półprostej AS i boku BC ( ? ) 4 Trójkąty o wspólnym wierzchołku i proporcjonalnej podstawie, muszą być podobne... Ale nie jestem pewien jak możnaby było to formalnie zapisać.

Ateusz: wydaje mi sie, ze to bedzie KBK

Ateusz: Bok kąt bok*

Ateusz: AP i PE leżą na wspolnym ramieniu AE CP i PB na CE kąt BPE=kąt APC a BE proporcjonalne z AC

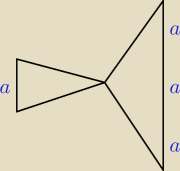
iteRacj@: 2/ Już chyba wiem, o jakie przekształcenie chodzi: symetria osiowa względem prostej zawierającej bok trójkąta. Jest to izometria. Podaj, który bok którego trójkąta jest osią symetrii. 3/ Punkty A,S,P są współliniowe z założenia, to wynika z treści. Ale czy pkt E też leży na tej prostej? To zależy od tego, w jaki sposób wybrałeś ten punkt, w rozwiązaniu powinno być jakieś wyjaśnienie. 4/ W tablicach maturalnych są podane warunki, jakie muszą spełniać trójkąty, żeby były podobne. Zawsze opieraj się na tym. Twój pomysł prowadzi do rozwiązania, ale brakuje opisu co, jak i z czego wynika.

iteRacj@: Zacznij tak: Przez pkt B prowadzę prostą równoległą do boku AC. Rysuję półprostą AP, przetnie ona prostą równoległa do boku AC w punkcie E. Teraz wykaż przystawanie ΔADS i ΔSBE. Następnie podobieństwo ΔACP i ΔPBE, ustal skalę podobieństwa.

Ateusz: 2. BC 3. punkt E to środek boku BA' w taki sam sposób jak punkt D boku AC. ΔADS przyst. ΔSBE. na mocy BKB DS=SB BE=AD i mają wspólny kąt ale do czego mi to w ogóle potrzebne?

iteRacj@: przystawanie ΔADS i ΔSBE ← moim zdaniem wynika z warunku KBK DS=SB // z treści zadania |<DSA|=|<ESB| kąty wierzchołkowe |<ADS|=|<BSE| dwie proste równowległe przecięte trzecią prostą wyznaczyły równe kąty naprzemianległe z przystawania wnioskuję, że pozostałe boki są trójkątów są odpowiednio równe ⇒ |DA|=|EB|=x (dopiero teraz wiem jaka jest długość |EB|) następnie należy uzasadnić że ΔAPC ~ ΔBPE i wtedy to co napisałeś 12:07 i dowód przeprowadzony

Ateusz: A czy to, że DA=EB=x nie wynika po prostu z własności równoległoboku? Są dwa równoległe i równe pary boków. Zatem AC = BA'

Ateusz: Według mnie to wszystko powinno wynikać z tego, że przedstawiona w 12:07 figura to konsekwencja odbicia symetrycznego trójkąta ABC względem BC, zatem wszystkie punkty i proste z trójkąta ABC będą takie same w BA'C, symetryczne.

Ateusz: dwie pary równoległych i równych boków*

iteRacj@: Ja ciągle nie wiem, co to jest to "odbicie symetryczne trójkąta ABC względem BC". NIe znam takiej izometrii. Najpierw myślałam, że to symetria osiowa względem prostej zawierającej bok trójkąta ABC. Z tego co piszesz 14:10, wynika, że chodzi o symetrię środkową względem środka boku CB. Wtedy z boków ΔABC i jego obrazu powstanie równoległobok, ale nadal trzeba wykazać, że obrazem punktu D będzie pkt E. Na pewno dorysowanie (bez żadnych symetrii) prostych równoległych, które utworzą równoległobok, dalej przystawanie ΔADS i ΔSBE, a potem podobieństwo ΔACP i ΔPBE + to co napisałeś 12:07 jest poprawnym dowodem.

Ateusz: No to nawet bez tej symetrii, czy skoro utworzyłem równoległobok, to czy nie wynika to po prostu z własności równoległoboku, że BA' to obraz AC po translacji o długość AB? Jest równoległobok −−> Są dwie pary równoległych, równych boków −−> AC=BA' −−> D'=środek AC, E=środek BA'

iteRacj@: Jeżeli w opisany sposób utworzysz równoległobok ABCA', to jest prawdą, że w translacji o wektor AB^→ obrazem odcinka AC będzie BA'. Obrazem punktu D, który jest środkiem boku AC będzie środek boku BA'. Stanie się tak dlatego, że translacja jest izometrią i zachowuje proporcje odległości. Ale pkt E nie został wybrany jako środek boku BA', jest to punkt w którym półprosta AP przecięła ten bok. Dlatego musisz wykazać, że przecięła akurat w połowie czyli że pkt E i środek boku BA' to ten sam punkt. Trzeba to pokazać, bo na tym opiera się Twój dowód.

Ateusz: ok, teraz rozumiem czyli : trojkaty asd bse przystaja na mocy kbk, pozaznaczam na rysunku kąty, to samo jesli chodzi o podobienstwo APC BPE, tak samo bkb tak? i wtedy dowod bedzie ok?

Ateusz: kbk* a z ciekawosci, moze ktos wie ile punktow moznaby mi bylo przyznac na maturze za taki dowod, w ktorym nie udowodnilem ze przedluzenie AP przechodzi przez srodek boku B'A?

iteRacj@: Podobieństwo ΔAPC i ΔBPE można wykazać na podstawie kbk, nie widzę innej proporcjonalności boków poza |CA|=2x i |BE|=x, a kąty są równe (wierzchołkowe i naprzemianległe). A potem to, co napisałeś na początku.