Misiu pomozesz mi? jolka: Misiu pomozesz mi?

Miś: a jakie to zadanie?

jolka: : W ostrosłupie prawidłowym sześciokątnym wysokosc jest o 50% dłuższa od krawedzi podstawy. Oblicz miarę kąta nachyllenia ściany bocznej do płaszczezny podstawy tego osrosłupa.

jolka: nie moge wogole pojec tych ostroslupow:(

Miś: hmm trudne to ma w podstawie 6kąt foremny tak?

jolka: tak tak foremny

jolka: i jak umiesz cos zrobic

Miś: masz do tego odp chyba 56 stopni

jolka: o blisko blisko ja mam odp 60stopni a jak to robiles?

jolka: moze jakas pomylka w obliczeniach

Miś: h=a+50%a=1,5a h=1,5a tgα=^1,5a_a=1,5 tg56stopni=1,5

jolka: dziekuje slicznie misiaku ja sobie zaraz to posprawdzam Dzieki bardzo

Miś: widocznie źle je zrobiłem skoro 60

justyś: i jak pomożesz

Miś: no nie wiem nie potrafię go zrobić chyba musze zacząć swoje robić zaraz

jolka: a czekaj chwile zaraz zobacze Misiu a jeszcze jedne mi pomozesz zrobic?

Miś: pokaż

jolka: Krawędz boczna ostrosłupa prawidłowego trójkątnego jest 2 razy dłuższa od krawedzi jego podstawy. Oblicz cosinusa kąta między ścianą boczną i podstawą ostrosłupa

jolka: i jak?

jolka: hehe a w tamtym mi wyszło 61 stopni jak liczyłam po swojemu tzn podobnie jak ty ale troche inaczej

justyś: jolu ty jesteś w 3 kl tak? napisz mi które zadanie str ok

jolka: tak tak w 3 ale to nie z ksiazki, nauczycielka nam dawala na kartkach takie zadanka

justyś: aha spr czy mam to zadanie

jolka: no dzieki Justys

jolka: Miś chyba już nam uciekł

justyś: Pp=a2 Pp=2*2 Pp=4cm

justyś: Pb=4* jedna druga a*h

justyś: Pb=4*jedba druga *3*6 Pb =2*18+=72 chyba dobrze nie jestem pewna

bartek: to pierwsze zadanie jest zle zrobione i ma wyjsc 60 stopni

bartek: h jest dobrze i ma wynosic 1.5a

	1.5a
Natomiast tgα=		=√3 ⇒ α=60
	a√32

jolka: O bartuś a umiesz je zrobić

Miś: oo już wiem gdzie mój błąd

jolka: a ja nie wiem dalej skąd to sie pobrało...

jolka: Bartek a skąd te a√3 sie wzieło?

Miś: to jest wysokośc trójkąta równobocznego, w tym przypadku tego takiego malutkiego, z których sześciu składa się podstawa

jolka: a już wiem widzicie i nie było wcale takie trodne co dwie głowy to nie jedna dzieki wam chłopcy

bartek:

	a√3
wysokosc trojkata rownobocznego:
	2

jolka: no juz wiem A te drugie spróbujecie jeszcze zrobic?

bartek: a jaki ma byc wynik?

jolka: własnie do tego nie mam::(

bartek:

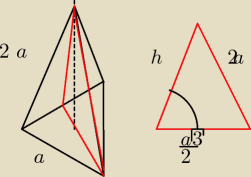
	√15a
z tw Pitagorasa wynika ze h=
	2

Teraz korzystamy z tw cosinosow:

	a√3		a√3
(2a)2=h2+(		)2−2h		cosα
	2		2

	1		√5
Po wyliczeniu wyszlo mi ze cosα=		=
	√45		15

jolka: dziekuje Bartus

bartek: nie gwarantuje ze jest dobrze, liczylem na szybko wiec nie wykluczam bledow w obliczeniach

jolka: hehe ja zaraz se na spokojnie zobacze i sprawdze ale cos mi sie wydaje ze ok bedzie Zdolny chłopak z Ciebie Bartusiu hihi dzieki