Okregi San Tropes: Dane sa okregi o(A r₁) i o(B,r₂) gdzie r₁<r₂ takie ze r₂−r₁<|AB|<r₁+r₂ Zilustruj zbir tych wszystkich punktow X ktorespelniaja warunki a) |AX|,r₁ i |BX|<r₂ b) |AX|≤r₁i |BX|>r₂ c) |AX|≥r₁ i |BX|= r₂ Wem tylko ze te okregi beda sie przecinac

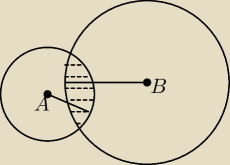
San Tropes: a) |AX|<r₁ i |BX|<r₂ a) bym sobie tak wyobrazal b i c poprosze o rozwiazanie

iteRacj@: Jeżeli dane jest koło k(A, r₁), to zbiorem punktów X spełniających nierówność |AX|<r₁ jest wnętrze tego koła, ponieważ jest to zbiór punktów, których odległość od środka koła jest mniejsza niż długość promienia. (Tak łatwiej te zależności zapamiętać.) Zbiorem punktów X spełniających równanie |AX|=r₁ jest okrąg o(A, r₁), będący brzegiem tego koła. Zbiorem punktów X spełniających nierówność |AX|>r₁ jest zewnętrze tego koła, ponieważ jest to zbiór punktów, których odległość od środka koła jest większa niż długość promienia.

San Tropes: Tylko tutaj mamy okregi .

iteRacj@: okrąg o(A, r₁) dzieli płaszczyznę na trzy części: 1/ zbiór punktów, których odległość od środka okregu jest mniejsza niż długość promienia tego okręgu czyli wnętrze koła k(A, r₁), 2/ punkty należące do okręgu o(A, r₁), ich odległość od środka okręgu jest równa promieniowi, 3/ zbiór punktów, których odległość od środka okręgu jest większa niż długość promienia czyli zewnętrze koła k(A, r₁) a/ odp. to obszar, który zaznaczyłeś bez brzegu ← nie ma równości

San Tropes: Dzieki . Masz duze wiadomosci .

iteRacj@: Niestety tylko na temat okręgu na płaszczyźnie.

San Tropes: To wystarczy . na maturze sa okregi , kąty w kole , styczne do okregu i okregow .

iteRacj@: Spróbuj odpowiedzieć na pyt. b/ i c/.

San Tropes: Bede sie zastanawial Prosze spojrzec na moj post o prostych k i l nizej .

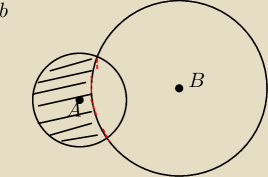
San Tropes: bez tego brzegu okregu o(B,r₂) zaznaczonego na czerwono

iteRacj@: b/ się zgadza

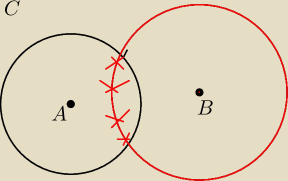
San Tropes: Ten brzeg okregu o(Br₂) zaznaczony na czerwono Tak to sobie wyobrazam

iteRacj@: Tak, łącznie z punktami wspólnymi obu okręgów (ponieważ są dwie równości).

San Tropes: Dzieki za pomoc