mam problem z rozwiązaniem zadania ika: Dla pięciu osób nakryto stół a nakrycie dla każdej z osób która do stołu zasiądzie jest innego koloru jeno żółte, drugie niebieskie trzecie zielone czwarte fioletowe piąte pomaranczowe. Do stołu zasiądą panowie X i Y oraz panie A, B i C Pan X nigdy nie siada obok pani A. Na ile sposobów można rozmieścić te pięć osób tak aby Pan X i pani A nie siedzieli obok siebie?

wredulus_pospolitus: 1) Siada Pan X ... skoro nakrycia są różne, to znaczy że miejsca są rozróżnialne −−− więc ma 5 możliwych miejsc 2) Siada Pani A ... skoro nie może siedzieć obok X to ma tylko dwa możliwe miejsca −−− 2 możliwości 3) Siadają pozostali na (łącznie) 3! sposobów mnożysz ... kooooniec

ika: Dziękuję bardzo👍

ika: Nie rozumiem zależności róznorodnosci naczyń, gdyby nakrycia były jednakowe, Pan X miałby wiecej mozliwych miejsc?

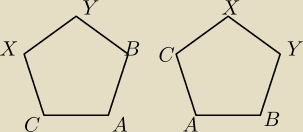
wredulus_pospolitus: Gdyby miejsca byłyby jednakowy to pierwszy siadający (Pan X) miałby tylko 1 możliwość posadzenia swoich czterech liter (ponieważ wszystkie miejsca są jednakowe, stół jest okrągły − więc gdzie by nie usiadł to i tak to jest 'to samo miejsce' i dopiero później on staje się punktem odniesienia Innymi słowy −−− te sytuacje (w momencie gdy miejsca są nierozróżnialne) nie są liczone jako inne możliwości usadzenia, a przy rozróżnialnych miejscach będą traktowane jako inne układy.

ika: Dziękuję, już rozumiem😄