zadanko JSNZ: Dla jakich m równanie log₃(x−m)+log₃x=log₃(3x−4) ma jedno rozwiązanie w zbiorze liczb rzeczywistych?

iteRacj@: dla m=1 → x=2

JSNZ: ?

Jerzy: log₃[(x−m)*x] = log₃(3x − 4)] x² − mx = 3x − 4 x² − mx − 3x + 4 = 0 x² −(m + 3)x + 4 = 0 Δ = 0 ⇔ (m + 3)² − 16 = 0 ⇔ m² + 6m + 9 − 16 = 0 ⇔ m² + 6m − 7 = 0 Δ_m = 36 + 28 = 64 m₁ = 1 lub m₂ = − 7 x² − (1 + 3)x + 4 = 0 ⇔ x² − 4x + 4 = 0 ⇔ x = 2 i 2 − 1 > 0 x² − (−4)x + 4 = 0 ⇔ x² + 4x + 4 = 0 ⇔ x = x = 2 i 2 + 7 > 0 Odp: m = 1 lub m = −7

Maciess: m = −7 odpada jak wczoraj przeliczałem. Wynik wychodzi x=−2 a taki x nie nalezy do dziedziny.

Jerzy: Racja, moja pomyłka.

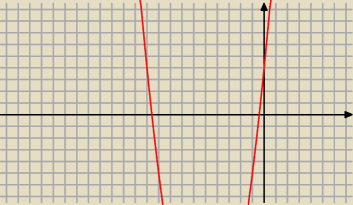
wredulus_pospolitus: ani jedno ani drugie rozwiązanie nie jest dobre 1) zał.

	4
x >
	3

x > m 2) x² − (m+3)x + 4 = 0 2.a) Δ = 0 −> m = 1 (to x = 2 −− ok) ; m = −7 (to x = −2 −−− nie ok) 2.b) Δ > 0 m²+6m −7 > 0 −> m∊(−∞ , −7) u (1, +∞) dla m>1

	m+3
xwierzchołka =		> 0
	2

f(x) = x² − (m+3)x + 4 ; f(0) = 4 > 0 brak rozwiązań dla m<−7

	m+3
xwierzchołka =		< 0
	2

f(x) = x² − (m+3)x + 4 ; f(0) = 4 > 0 sprawdzamy kiedy drugie nie będzie w dziedzinie, a drugie w dziedzinie

	(m+3) + √(m+7)(m−1)		4
x1 =		> −
	2		3

	(m+3) − √(m+7)(m−1)		4
x2 =		< −
	2		3

(jeszcze trzeba 'dla pewności' sprawdzić aby x₁ > m co akurat jest spełnione (dla tego przedziału m) gdy tylko x₁ > − 4/3) i np. n = −13 f(x) = x² + 10x + 4

	16		40		16 − 120 + 36
f(−4/3) =		−		+ 4 =		< 0
	9		3		9

	4
czyli jedno z miejsc zerowych funkcji f(x) jest w przedziale (−		; 0)
	3

wredulus_pospolitus:

	4		4
ajjjj ... teraz zauważyłem że pod drodze zmieniłem z +		na −
	3		3

JSNZ: Czyli od 4/3 do ∞?

Jerzy: Postaw sobie np. m = 2 i zobacz, co sie bedzie działo.

JSNZ: Proszę wytłumaczcie mi to

wredulus_pospolitus: 1) sprawdzamy kiedy równanie x² − (m+3)x + 4 = 0 będzie miało DOKŁADNIE jedno rozwiązanie (patrz co zrobił Jerzy). 2) sprawdzamy czy ów rozwiązanie ( 'x' ) spełnia warunki jakie stawia przed nami liczba logarytmowana (odrzucamy w tym momencie jedna z 'm' ) 3) sprawdzamy czy może istnieć taka sytuacja, że równanie x² − (m+3)x + 4 = 0 będzie miało dwa rozwiązania, ale jedno z nich będzie odrzucane ze względu na warunki z logarytmów, a drugie będzie spełniać warunki które mamy z logarytmów. (i tu odpowiedź brzmi − nie ... nie ma takiej możliwości −−− co możesz spróbować samodzielnie pokazać (nie trzeba rozwiązywać równania) )

JSNZ: Jak nie jak np dla m=8 jest spełnione a nie wynika to z 1)

wredulus_pospolitus: no to widzisz ... musisz sprawdzić jeszcze (3) ... możesz się ograniczyć do przedziału m > 1

	4
i sprawdzić kiedy jedno z miejsc zerowych będzie w przedziale 0 < x1 ≤
	3

do dzieła

wredulus_pospolitus: pamiętaj, że x₂ > m

JSNZ: No tak ale jak to policzyć żeby jedno było w dziedzinie a drugie nie? mamy (x₁>4/3 i x₁>m) i (x₂<4/3 lub x₂<m)?

JSNZ: no i m∊(−∞ , −7) u (1, +∞)

JSNZ: Ze wzorów vieta to nie wychodzi...