Wielomian Domek: Wyznacz zbiór wszystkich punktów P(a,b) płaszczyzny jeśli wiadomo że a i b są wartościami parametrów przy których równanie a⁴x³ −3a² x +b =0 ma dokładnie 3 rózne pierwiastki rzeczywiste. Narysuj otrzymany zbiór

ICSP: III różne pierwiastki rzeczywiste, wiec wyróżnik musi być ujemny. Dlatego zamiast równania Δ = 0 rozwiązujesz Δ > 0. Dużo się nie zmieni.

ICSP: Na odwrót. Wyróżnik dodatni, więc rozwiązujesz Δ < 0.

Mila: Oj, tak 3 różne rzeczywiste , to Δ<0.

Mila: Miło, że spojrzałeś.

lol: w wielomianie 3 stopnia Δ na poziomie liceum?

ABC: nie słyszałeś o wyróżniku dla równania trzeciego stopnia? zresztą to zadanie można z pochodnych zrobić na poziomie liceum

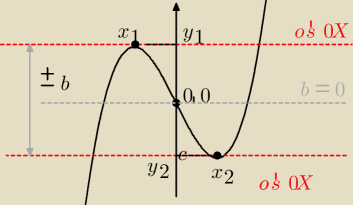
ite: Co zmienia wartość współczynnika b i jakie mu nadać wartości ← na rysunku. 1/ a=0 → f. liniowa brak rozwiązań 2/ a≠0 f(x)= a⁴x³ −3a² x+b f'(x)= 3a⁴x² −3a²=3a²(a²x²−1)=3a²(ax−1)(ax+1)

	1		−1
x1=		, x2=		teraz sprawdzenie, czy są to ekstrema.
	a		a

Następnie należy wyliczyć drugie współrzędne i ustalić wartości parametru b.