 blicz przybliżoną miarę kąta między przekątnymi prostokąta,
w którym długość jednego z boków stanowi 75% długości drugiego boku.
Zrobi ktoś i wytłumaczy? B)
blicz przybliżoną miarę kąta między przekątnymi prostokąta,
w którym długość jednego z boków stanowi 75% długości drugiego boku.
Zrobi ktoś i wytłumaczy? B)
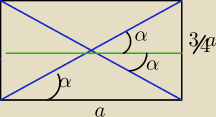 d=√a2+9/16a2=5/4a
sinα=(3/4a)/(5/4)a=3/5
α≈37 stopni
2α≈74 stopnie
d=√a2+9/16a2=5/4a
sinα=(3/4a)/(5/4)a=3/5
α≈37 stopni
2α≈74 stopnie
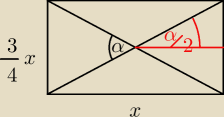 oznaczmy ten mniejszy kat jako α
Dluzszy bok niech bedzie x, wtedy ten drugi 0,75x czyli (3/4)*x
z Pitagorasa przekatna :
9/16 x2 + x2 = c
25/16 x2 = c
c = (5/4) * x = 1,25x
polowa przekatnej to
oznaczmy ten mniejszy kat jako α
Dluzszy bok niech bedzie x, wtedy ten drugi 0,75x czyli (3/4)*x
z Pitagorasa przekatna :
9/16 x2 + x2 = c
25/16 x2 = c
c = (5/4) * x = 1,25x
polowa przekatnej to
| (5/4)x | 5 | ||
= | x | ||
| 2 | 8 |
| 3 | ||
połowa długości | x | |
| 4 |
| 5 | ||
podzielona przez połowa przekątnej czyli | x | |
| 8 |
| 3 | 3 | |||
połowa długości | x = | x | ||
| 4 | 8 |
| 3 | 8 | 3 | |||||||||||
sin (α/2) = | = | * | = | = 0,6 | ||||||||||
| 8 | 5 | 5 |
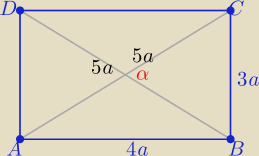 |AB|=4a , |BC|=3a to |AC|=|BD|=5a
|AB|=4a , |BC|=3a to |AC|=|BD|=5a
| 1 | ||
P=4a*3a=12a2 i P= | *5a*5a*sinα | |
| 2 |