Pochodna
Grzegorz:
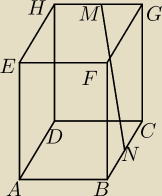
Rozważamy wszystkie graniastosłupy prawidłowe czworokątne
ABCDEFGH takie, że odcinek MN, który łączy środki krawędzi BC i GH, ma długość 12.
Oblicz długości krawędzi tego z rozważanych graniastosłupów, który ma największą objętość.
20 mar 17:52
a7: może coś na początek:
oznaczamy podstawę a, wysokość H
122=(a22)+√H2+(a22)
V=a2*H
20 mar 19:02
a7: 122= (a2)2+(√H2+(a2)2)2
20 mar 19:08
a7: ?
20 mar 19:08
Mila:
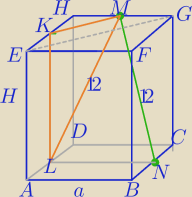
W ΔLKM:
2)
V=a
2*H
| | a2 | |
V=a2*√144−a2/2 i 144− |
| >0⇔a∊(0,12√2) |
| | 2 | |
| | −a | |
V'(a)=2ap{144−a2/2)+a2* |
| |
| | 2√144−a2/2 | |
V'(a)=0⇔ 576a−3a
3=0 ⇔a*(576−3a
2)=0
a=0 lub a
2=192
a=
√64*3=8
√3 lub a=−8
√3
dla a=8
√3 funkcja V(a) ma maksimum, pozostałe a nie należą do dziedziny
(uzasadnij)
H=
√144−96=
√48=4
√3
V=192*4
√3=768
√3 [j
3]
================
Sprawdzajcie rachunki
20 mar 21:37
Grzegorz: pochodna od √x jest równa 12√x a u ciebie ta 1 równa się −a? Chodzi mi o linjke ,w
której liczysz pochodną
21 mar 17:03
Mila:
| | 1 | | 1 | |
(√144−a22)'= |
| *(144− |
| a2)'= |
| | 2√144−12a2 | | 2 | |
| | 1 | | 1 | |
= |
| *(− |
| *2a)= |
| | 2√144−12a2 | | 2 | |
21 mar 17:45
 Rozważamy wszystkie graniastosłupy prawidłowe czworokątne
ABCDEFGH takie, że odcinek MN, który łączy środki krawędzi BC i GH, ma długość 12.
Oblicz długości krawędzi tego z rozważanych graniastosłupów, który ma największą objętość.
Rozważamy wszystkie graniastosłupy prawidłowe czworokątne
ABCDEFGH takie, że odcinek MN, który łączy środki krawędzi BC i GH, ma długość 12.
Oblicz długości krawędzi tego z rozważanych graniastosłupów, który ma największą objętość.
