Geometria przestrzenna TSP: Prostokąt o bokach długości a i b (a<b) obraca się dookoła prostej leżącej w płaszczyźnie prostokąta, nie przecinając prostokatą, równoległej do dłuższego boku i odległej od niego o c. Wyznacz pole powierzchni całkowitej i objętość bryły powstałej przez obrót prostokąta. Wyszło mi P=2π(a+c)((a+c)+b) oraz V=π(a+c)²b, jednak w odpowiedziach jest kompletnie inny wynik. Czy mógłby mi ktoś to wytłumaczyć?

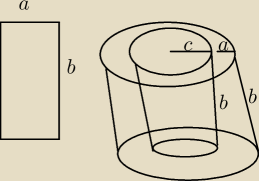
a7: to będzie taki walec bez walca w środku V=π(a+c)²*b−πc²*b=πab(a+2)

a7: ?

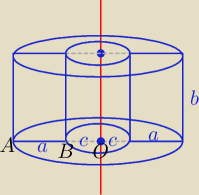
Mila: To jest rura ( pusta w środku) − |AO|=R=a+c r=|BO|=c 1) V=πR²*b−πr²*b=π*b*(R²−r²)=π*b*[(a+c)²−c²]= π(a²+2ac)*b 2) Pole powierzchni: P_b=2πR*b+2π*r*b=2π*b(R+r)=2πb*(a+2c) Pole pierścienia : P_p=πR²−πr²=π*(R²−r²)=π*[(a+c)²−c²]=π*(a²+2ac) P_c=2πb*(a+2c)+2π*(a²+2ac) ===================== Czy się zgadza teraz, może jest pomyłka?

a7: P=π(a+c)b+πcb +π(a+c)²−πc²=...

a7: w obliczeniu P jest oczywiście błąd przepraszam P=2π(a+c)b+2πcb +π(a+c)2−πc2 = chyba teraz dobrze