POOOMOOCYYY efka: Dane są punkty A=(−1;0) B=(k²;1) C=(−2;−3k). Dla jakiej wartości parametru k proste AB i AC są prostopadłe?

Mila: AB^→=[k²+1,1] AC^→=[−1,−3k] [k²+1,1] o [−1,−3k]=0 iloczyn skalarny wektorów równy 0. −k²−1+1*(−3k)=0 −k²−1−3k=0 k²+3k+1=0 dokończ sama

efka: Odpowiedzi w książce podają,że k=¹₂ lub k=1,a pierwiastek z delty wychodzi mi √5 więc dalej też mi wychodzi dziwny wynik

Mila: Dobrze przepisane zadanie? Zaraz sprawdzę.

efka: Tak, wszystko dobrze przepisane. Sama wcześniej policzyłam i również doszłam do takiego równania z deltą, ale nie zgadzał mi się wynik z odpowiedziami, dlatego zgłosiłam się tutaj, ale może jest po prostu błąd w odpowiedziach

Mila: Z jakiej książki?

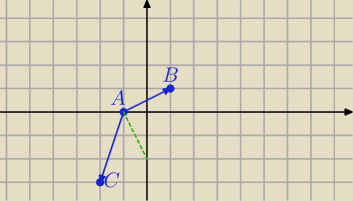
Mila: Jeżeli podstawimy wartości k z odpowiedzi to otrzymamy punkty: dla k=1 A=(−1,0), B=(1,1), C=(−2,−3) jak widzisz prostopadłości nie ma

efka: książka matematyka z sensem dziękuję serdecznie za pomoc!