Planimetria asd: Wyznacz sinusy kątów ostrych trójkąta prostokątnego wiedząc, że stosunek promieni okręgów

	13
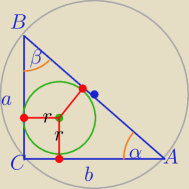
opisanego i wpisanego w ten trójkąt jest równy		.
	4

Widziałem już https://www.zadania.info/d141/3945452 te rozwiązanie,ale zastanawia mnie,czy da się to zrobić jakoś inaczej

	abc		ab		r(a+b+c)		c
kombinując wzorami		,		,		,R=
	4R		2		2		2

Mila:

R		13		13
	=		⇔R=		r
r		4		4

	13
|AB|=2R=		r
	2

1) Suma długości przyprostokątnych jest równa sumie dł. średnic okręgó wpisanego i opisanego na Δ prostokątnym

	17		13
a+b=2r+2R⇔a+b=		r /:(		r)
	2		2

a		b		17
	+		=		⇔
13   ( r)   2		13   ( r)   2		13

	17		289
sinα+cosα=		/2⇔2sinα*cosα=		−1
	13		169

	60
sinα*cosα=
	169

	17		60
sinα*(		−sinα)=		, sinα∊(0,1)
	13		169

dokończ