Prosta styczna do okręgu john: Punkt A = (2, −1) należy do środka okręgu S = (4, −2), wyznacz równanie stycznej do tego okręgu przechodzącej przez punkt A Wiem że znacznie szybciej można by to obliczyć z układu równań, ale chce wiedzieć gdzie mam błąd. Najpierw obliczyłem promień okręgu a potem wykorzystałem wzór na odległość prostej od okręgu korzystając z faktu że przechodzi przez A. r = √(4 − 2)² + (−2 − 1)² = √13 y = ax + b −1 = 2a + b b = −1 − 2a y = ax − 1 − 2a −ax + y + 1 + 2a = 0

−4a − 2 + 1 + 2a
	= √13
√a2 + 1

−2a − 1
	= √13 |()2
√a2 + 1

4a2 + 4a + 1
	= 13
a2 + 1

4a2 + 4a + 1 − 13a2 − 13
	= 0
a2 + 1

−9a² + 4a − 12 = 0 Δ = 16 − 4 * (−9) * (−12) = 16 − 432 ..... czyli wynika z tego że nie ma rozwiązań, nie mogę doszukać się błędu, pomocy

Jerzy: Zacznij od początku.Przecież to absurd.Jak punkt może należeć do środka okręgu ? To ten sam punkt ?

john: tam powinna być wartość bezwzględna w liczniku ale to nic tutaj nie zmieni

john: Oj sory, miało być należy do okręgu o środku

john: Już wiem że tak można tylko chciałem wiedzieć gdzie mam błąd

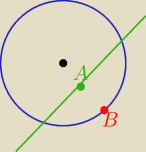
Mila: Popraw treść. Każda prosta przechodząca przez A przecina okrąg w dwóch punktach, więc nie może być styczną. Może punkt należy do okręgu? Przykład punkt B.

john: Tak punkt należy do okręgu

john: puk puk

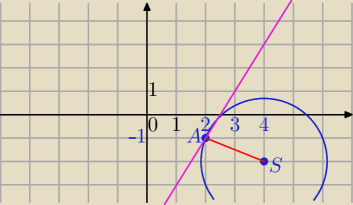
Mila: A = (2, −1) należy do okręgu ośrodku S = (4, −2) r=√2²+1²=√5 Styczna prostopadła do AS i przechodząca przez A. SA^→=[2,1]− wektor prostopadły do stycznej

	2
s: y=		x+b i A∊s
	1

−1=2*2+b, b=−5 s: y=2x−5 równanie stycznej II sposób odległość punktu S od prostej jest równa r y=ax+b , A∊prostej −1=2a+b, b=−1−2a y=ax−1−2a s: ax−y−1−2a=0

	|a*4+2−1−2a|
D(s,S=(4,−2))=		=√5
	√a2+1

|2a+1|=√5*√a²+1 /² 4a²+4a+1=5a²+5 a²−4a+4=0 (a−2)²=0 a=2 s: y=2x−5 ========= Eta ma ładny wzór na styczną przechodzącą przez punkt okręgu.

john: Wybaczcie za późny odzew, dzięki za odpowiedź Mila

iteRacj@: Eta możesz podać ten wzór na styczną przechodzącą przez punkt okręgu?

Eta: Hej ite o: ( x−a)²+(y−b)²=r² i A(x_A,y_A) ∊ o to styczna w punkcie A ma równanie s: (x−a)(x_A−a)+(y−b)(y_A−b)=r²

john: Eta możesz dać jakieś źródło do tego wzoru albo nakierować skąd to się wzięło?

iteRacj@: dziękuję! i już stosuję : )

john: W sensie widać że z równania okręgu ale czemu to działa to ja nie wiem

Ateusz: @Eta czy moge cos takiego zastosowac na maturze jako oczywista wlasnosc?

Eta: Jasne,że możesz

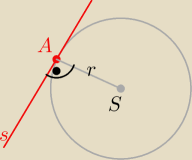
Eta: Podaję wyprowadzenie tej zależności S(a,b) , r=|SA| Punkt A musi leżeć na okręgu ! A(x_A,y_A) ∊o to (x_A−a)²+(y_A−b)²=r² i prosta AS : (x_A−a)(x−x_A)+y_A(x_A−a)=0 dodając stronami po przekształceniach otrzymujemy: .................. s: (x−a)(x_A)+(y−b)(y_A−b)=r²