 Mam pytanie odnośnie mojego sposobu
W trójkącie ABC AC=7, BC=8 zaś ∠ABC=60∘ . Oblicz V bryły powstałej z obrotu trójkąta ABC wokół
prostej zawierającej bok AC.
1) Wyliczyłem, że AB równa się 3 lub 5
i teraz tak
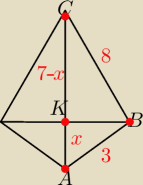
|AK|=x
|CK|=7 − x
|KB|=r
2) Z tw pit. w ΔKAB
x2+r2=9 ⇒ r2=9−x2
3) Z tw. pit w ΔCKB
(7−x)2+r2=64
r2=64−(7−x)2
4) Z 2 i 3
Mam pytanie odnośnie mojego sposobu
W trójkącie ABC AC=7, BC=8 zaś ∠ABC=60∘ . Oblicz V bryły powstałej z obrotu trójkąta ABC wokół
prostej zawierającej bok AC.
1) Wyliczyłem, że AB równa się 3 lub 5
i teraz tak
|AK|=x
|CK|=7 − x
|KB|=r
2) Z tw pit. w ΔKAB
x2+r2=9 ⇒ r2=9−x2
3) Z tw. pit w ΔCKB
(7−x)2+r2=64
r2=64−(7−x)2
4) Z 2 i 3
| 3 | ||
9−x2=64−(7−x)2⇒ x=− | i tutaj jest mój problem, ponieważ x nie może być ujemny, ale jak | |
| 7 |
| 3 | ||
r2=9− (− | )2 | |
| 7 |
| 9 | ||
r2=9− | ||
| 49 |
| 432 | ||
r2= | ||
| 49 |
| 12√3 | ||
r= | ||
| 7 |
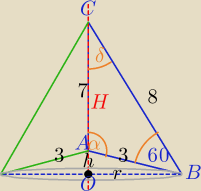 Z (1) wynika, że c=3 lub c=5.
Kąt γ ma najmniejsza wartość, jest ostry.
Trzeba zbadać jaki jest kąt przy wierzchołku A.
Z tw. cosinusów:
82=32+72−2*3*7 *cosα
Z (1) wynika, że c=3 lub c=5.
Kąt γ ma najmniejsza wartość, jest ostry.
Trzeba zbadać jaki jest kąt przy wierzchołku A.
Z tw. cosinusów:
82=32+72−2*3*7 *cosα
| 1 | ||
cosα=− | ⇔α− kąt rozwarty. | |
| 7 |
| 3 | 7 | ||
= | |||
| sinδ | sin60 |
| 3√3 | ||
sinδ= | ||
| 14 |
| r | 3√3 | r | 12√3 | |||||
sinδ= | ⇔ | = | ⇔r= | |||||
| 8 | 14 | 8 | 7 |
| 1 | 1 | |||
Vb= | π*r2*H− | π*r2*h= | ||
| 3 | 3 |
| 1 | 1 | 12√3 | ||||
= | π*r2*(H−h)= | π*( | )2*7 | |||
| 3 | 3 | 7 |
| 144π | ||
Vb= | [j3] | |
| 7 |
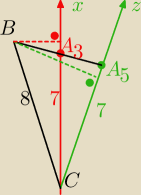 Rysunek jest zły osie obrotu są y lub z
Rysunek jest zły osie obrotu są y lub z