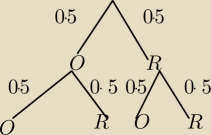
Prawdopodobienstwo ja: W pudełku znajduje sie 6 kul czarnych i 4 kule białe. Rzucamy dwa razy moneta. Jesli otrzymamy 2 orły, losujemy z pudełka kolejno bez zwracania 2 kule. W pozostałych przypadkach losujemy jedna kule. Oblicz prawdopodobienstwo, ze wsród wylosowanych kul jest dokładnie jedna kula czarna. Co jest złego w moim rozwiązaniu i dlaczego pewnie wszystko?Nie pogardze też inną metodą,ale chce wiedzieć co tutaj jest źle też A.Dwa orły i dobieramy bez zwracania dwie kule (dokładnie jedna kula czarna,czyli druga musi byc biala):

10 2
	=45 (dwie kule z 10)

	1		1		6*4
P(A)=		*		*
	2		2		45

B.W pozostalych przypadkach jedna kule (czyli musza byc same czarne z 10 kul ktore mamy w puli)

	1		1
P(B)=3*		*
	4		10

	5
No i po zsumowaniu prawdopodobieństw zajść zdarzeń A i B wychodzi		,co jest blednym
	24

wynikiem.Prosze o pomoc

Jerzy: A)

	1		1		6*4
P(A) =		*		*
	2		2		10*9

B)

	1		6
P(B) = 3*		*
	4		10

ja:

	6
Dlaczego w B) jest mnożone *		?
	10

Jerzy: Poprawa do A)

	1		1		6*4 + 4*6
p(A) =		*		*[		]
	2		2		10*9

Jerzy: Bo wśród dziesięciu kul jest 6 czarnych i każdą z nich mozesz wylosować z jednakowym prawdopodobieństwem.

ja: No przecież..Dziękuje za pomoc