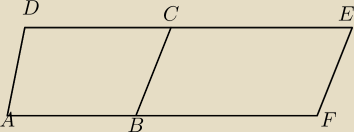
Rownolegloboki 6latek: Dwa nieprzystajace rownolegloboki ABCD i BCEF maja wspolny bok BC Wykaz z e czworokat ADEF jest tez rownoleglobokiem czy rysunek do zadania bedzie wygladal tak ? Np AB<BF?

wredulus_pospolitus: Skoro AD || BC oraz BC || EF to AD || EF

6latek: Czyli moze byc taki rysunek . dziekuje Prosze sprawdz to poprzednie zadanie .

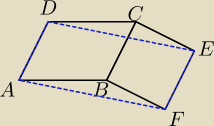
wredulus_pospolitus: Ale rysunek to raczej tak winno się zrobić: I musisz wykazać, że DE || AF

wredulus_pospolitus: Jak widzisz ... C nie musi należeć do odcinka DE

6latek: No to zes teraz wymyslil Nie wiem jaka ceche wziac aby te trojkaty byly przystajace Dwa boki mam rowne ale brakuje mi trzeciej

wredulus_pospolitus: tą samą co w tamtym zadaniu znasz kąty: ∡DCB oraz ∡BCE więc znasz ∡DCE ... wykazujesz że ∡ABF jest jemu równy wiesz, że |DC| = |AB| oraz |CE| = |BF| więc lecisz z przystawania trójkątów

6latek: Juz chyba widze kąt DCE= kątowi ABF DC= AB CE=BF stad DE= AF Wobec rownosci par bokow DE=AF i AD= EF DEIIAF

wredulus_pospolitus: Pytanie −−− skąd wiesz, że: kąt DCE= kątowi ABF (masz rację ... ale trza to jakoś wykazać

6latek: Popatrzylem na rysunek zaraz to sobie zobacze co napisales wyzej . dziekuje CI

an: Z definicji Równoległobokiem nazywamy czworokąt, w którym przeciwległe boki są parami równoległe. Mamy dwa równoległoboki mające wspólny bok to AD||BC oraz BC||EF dwa odcinki z których każdy jest równoległy do trzeciego są do siebie równoległe AD||EF. AD=BC oraz BC=EF to i AD =EF Proste przechodzące odpowiednio przea AE oraz DF są równogłe gdyż odległości między nimi są jednakowe (wynika to z jednakowych kątów pod którymi się przecinają) Więc mamy boki parami równoległe, czyli czworoką jest równoiległobokiem.cnw.

6latek: Witam an czyli odniosles sie do mojego pierwszego rysunku ?

6latek: Ale wredulus tez podal dobry przyklad ewentualnego rysunku . U niego musze wykorzystac przystawanie trojkatow .

6latek: Blee Nie wiem jak mam wykazc ze kąt ABF = kątowi DCE Myslalem ze wiem

an: Odniosłem się do wypadku ogólnego czyli do tego co narysował @wredulus_pospolitus Ja nie jestem nauczycielem, moim zdaniem wykazanie, że odpowiada przyjętej definicji jest wystarczające co nie znaczy, że to co tu napisałeś jest źle, ale w/g mnie jest to wyważanie otwartych drzwi. On pokazał, że Twój rysunek jest tylko jedną z możliwości i to szczególną, jego jest przypadkiem ogólnym nieskończenie wielu możliwości w tym Twoją. Zauważ, że punkty BC tylko w tym szczególnym wypadku leżą na bokach powstałego równoległoboku w pozostałych nie. Często po rozwiązaniu zadania okazuje się, że można było to zrobić prościej, wymaga to doświadczenia zdobywanego rozwiązywaniem zadań.

6latek: Dobrze

6latek: Jesli bym mial wykazane rownosci kątow DCF i ABF to wtedy z przystawania trojkatow (cecha BKB ) mam rownosc bokow DE i AF Wobec rownosci bokow AD i EF stwierdzam z e DEIIAF

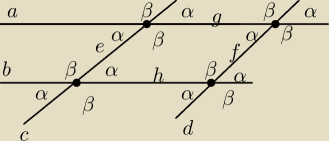
an: Jeżeli proste a||b i c||d, to kąty równe jak na rysunku i odcinki e=f oraz g=h, ale to chyba znasz trójkąty DCE i BCF są przystające z racji jw

6latek: Tak an znam to . Tylko chcialem to zrobic inaczej bo tak ∡ABC znam rowniez ∡FBC znam Teraz jak policzyc ∡AFB?

6latek: Czy jest ktos w stanie pomoc?

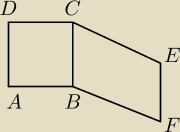
Jerzy: Cześć Trudno wykazać nieprawdę

6latek: Dzien dobry Jerzy Dlaczego tak twierdzisz ?

Jerzy: OK. Żle zinterpretowałem treść zadania 12:10 to jest poprawny rysunek.

6latek: Potrafisz powiedziec?

6latek: Musi byc prosty sposob

Jerzy: AD = EF , to oczywiste. Wystarczy wykazać,że AF || DE ( jak napisal wredulus )

6latek: Ale to musze wykazac ze DE=AF Zeby to wykazac musze najpierw wykazac ze ∡DCF=∡ABF A o to sie rozbija bank

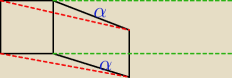
Jerzy: Raczej wykazć,że ∡DCE = ∡ABF ( a to pokazuje rysunek ) I prosto pokazujesz,że trójkaty DCE i ABF są identyczne.

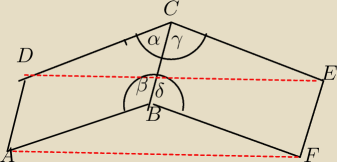
6latek: Dobrze A moze byc tak ? β=180−α δ= 180−γ ∡ABF=360−(180−α)−180−γ)= α+γ=∡DCE Teraz tak wymyslilem

Jerzy: ∡ABF = 360 − (β + δ) = 360 − [(180 − α) + (180 − γ)] = 360 − 180 + α − 180 + γ = α + γ = ∡ DCE

6latek: dzieki Tyle czasu siedzialem nad tym zadaniem