Geometria
Bolsz: Dany jest trapez rownoramienny ABCD, w ktory mozna wpisac okrag. Kat ADB jest katem prostym.
Wyznacz sinus kata jaki tworzy przekatna tego trapezu z jego dluzsza podstawa.
18 mar 09:56
Bleee:
Skoro ∡ADB to ten trapez rownoramienny jaka jest fugura? A skoro w tą figurę można wpisać okrąg
to jaka teraz jest figura? A ta figura ma przekątnej pod jakim kątem?
18 mar 09:59
wredulus_pospolitus:
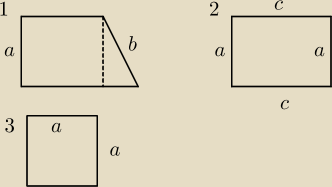
Albo jak wolisz:
1) Rysujemy dowolny trapez PROSTOKĄTNY
2) Ale ma być on też równoramienny, więc a = b
3) A skoro ma mieć wpisany okrąg to a+a = c+c −> a = c
18 mar 10:10
zys:
... co Ty wypisujesz

18 mar 10:57
zys:
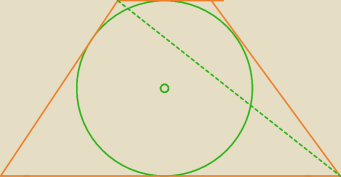
18 mar 11:06
wredulus_pospolitus:
zys −> Kat ADB jest katem prostym

18 mar 11:16
zys:
no właśnie ADB ... to oznacz porządnie wierzchołki

18 mar 11:21
wredulus_pospolitus:
Narysuj mi trapez równoramienny z kątem prostym ADB

18 mar 11:23
zys:
masz narysowany
18 mar 11:25
wredulus_pospolitus:
A kuźwa ... ja widziałem ∡AD
C a nie ADB

18 mar 11:25
wredulus_pospolitus:
tak to jest jak się treść czyta 'na tronie'

18 mar 11:26
zys:
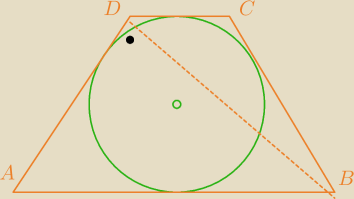
18 mar 11:29
zys:

18 mar 11:30
Bolsz: No dobra, ale jak dojsc do sinusa tej przekatnej?
18 mar 15:15
Eta:
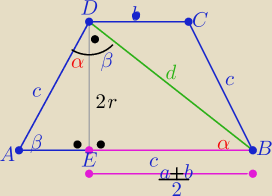
z warunku wpisania okręgu w trapez
z podobieństwa trójkątów AED i EBD (kkk)
| | 2r | | 4r2 | |
i w ΔAED cosα= |
| to cos2α= |
| |
| | c | | c2 | |
| | 2r | | 4r2 | |
w ΔEBD sinα= |
| ⇒ sinα= |
| |
| | d | | c2 | |
to sinα= cos
2α ⇒ sinα=1−sin
2α
sin
2α+sinα−1=0 i α kąt ostry
...............................
=================
18 mar 15:37
 Albo jak wolisz:
1) Rysujemy dowolny trapez PROSTOKĄTNY
2) Ale ma być on też równoramienny, więc a = b
3) A skoro ma mieć wpisany okrąg to a+a = c+c −> a = c
Albo jak wolisz:
1) Rysujemy dowolny trapez PROSTOKĄTNY
2) Ale ma być on też równoramienny, więc a = b
3) A skoro ma mieć wpisany okrąg to a+a = c+c −> a = c









 z warunku wpisania okręgu w trapez
z warunku wpisania okręgu w trapez