Geometria analityczna Bolsz: Dany jest trojkat o wierzcholkach A=(1,0), B(4,4) i C oraz polu rownym 5. Wyznacz wspolrzedne wierzcholka C wiedzac, ze wysokosc CD dzieli bok AB w ten sposob ze |AD| : |DB|= 1:4.

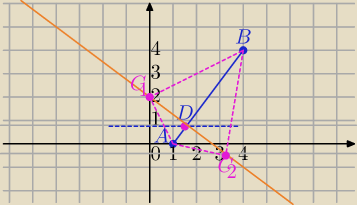
Mila: 1) AB^→=[3,4] |AB|=5

	1
PΔABC=5⇔		*5*h=5⇔h=2
	2

	1		3		4
AD→=		*[3,4]=[		,		]
	5		5		5

	3		4		4
A=(1,0)→T[		,		]⇒D=(135,		)
	5		5		5

2) Prosta DC⊥AB

	3		4		3		8
y=−		x+b⇔		=−		*		+b
	4		5		4		5

b=2

	3
y=−		x+2
	4

3)

	3
C=(c,−		c+2)
	4

	8		4		3
|CD|2=(		−c)2+(		−2+		c)2
	5		5		4

	8		3		6
(		−c)2+(		c−		)2=4
	5		4		5

1		1
	c2−		c=0
16		5

	16
c=0 lub c=
	5

	2
C=(0, 2) lub C=(315, −		)
	5

======================= posprawdzaj rachunki

wredulus_pospolitus: 1) |AB| =

	1
2) P =		*|AB|*|CD| −> |CD| = ...
	2

3) Masz proporcje ... wyznacz współrzędne punktu D 4) wyznacz wektor prostopadły do AB 5) Mając D, mając długość |CD|, mając wektor prostopadły ... wyznaczasz współrzędne punktu C