Romb
6latek: Wykaz ze wierzcholek rombu jest rowno oddalony od dwoch prostych nie przechodzacych przez ten
wierzcholek i zawierajacych boki rombu
Poprosilbym tylko o rysunek
16 mar 23:07
Eta:
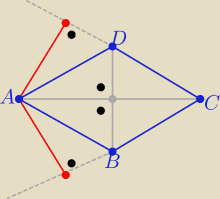
16 mar 23:18
6latek: Dziekuje

Dobranoc

16 mar 23:26
6latek:
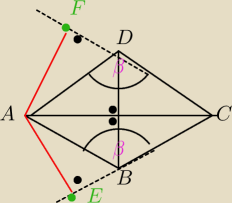
mamy udowodnic ze AE=AF
Najpierw pare uwag
Punkt E bedzie lezal za przedluzeniu boku BC
tak samo punkt F bedzie lezal na przedluzeniu boku CD
Odcinek AE bedzie ⊥ do CE
Odcinek AF ⊥CF
Z rownosci bokow AD i AB Wynika rownosc bokow EB i FD
∡FDA=∡ABE= 180
o−β
Wobec tych rownosci ΔAEB≡ΔAFD
Z przystawania tych trojkatow wynika rownosc bokow AE i AF i mamy teze
Czy tak wystarczy czy nalezy to inaczej rozpisac ?
17 mar 14:49
6latek:
17 mar 15:07
Pytający:
Punkt E bedzie lezal za przedluzeniu boku BC
tak samo punkt F bedzie lezal na przedluzeniu boku CD
Odcinek AE bedzie ⊥ do CE
Odcinek AF ⊥CF
Można to napisać krócej.
Niech punkty E, F będą odpowiednio rzutami wierzchołka A na proste BC oraz CD
Z równości boków AD i AB Wynika rownosc bokow EB i FD.
To nie jest prawda, w tym momencie skorzystałeś z przystawania trójkątów ABE oraz ADF
∡FDA=∡ABE= 180○−β
Tutaj jest okej dopisałbym tylko że jest to równe α
I tutaj inaczej:
ΔABE oraz ΔADF są trójkątami prostokątnymi. Wówczas ∠EAB=∠DAF=90−α.
Stąd ΔABE ≡ ΔAFD na mocy cechy kąt−bok−kąt.
i końcówka jest okej
Z przystawania tych trojkatow wynika rownosc bokow AE i AF i mamy teze
17 mar 16:50
6latek: Dziekuje Ci

17 mar 17:42

 Dobranoc
Dobranoc 
 mamy udowodnic ze AE=AF
Najpierw pare uwag
Punkt E bedzie lezal za przedluzeniu boku BC
tak samo punkt F bedzie lezal na przedluzeniu boku CD
Odcinek AE bedzie ⊥ do CE
Odcinek AF ⊥CF
Z rownosci bokow AD i AB Wynika rownosc bokow EB i FD
∡FDA=∡ABE= 180o−β
Wobec tych rownosci ΔAEB≡ΔAFD
Z przystawania tych trojkatow wynika rownosc bokow AE i AF i mamy teze
Czy tak wystarczy czy nalezy to inaczej rozpisac ?
mamy udowodnic ze AE=AF
Najpierw pare uwag
Punkt E bedzie lezal za przedluzeniu boku BC
tak samo punkt F bedzie lezal na przedluzeniu boku CD
Odcinek AE bedzie ⊥ do CE
Odcinek AF ⊥CF
Z rownosci bokow AD i AB Wynika rownosc bokow EB i FD
∡FDA=∡ABE= 180o−β
Wobec tych rownosci ΔAEB≡ΔAFD
Z przystawania tych trojkatow wynika rownosc bokow AE i AF i mamy teze
Czy tak wystarczy czy nalezy to inaczej rozpisac ?
