Graniastosłup prawidłowy czworokątny wpisany w stożek
madzia: W stożek o wysokości 5 i promieniu postawy 2√2 wpisano graniastosłup prawidłowy czworokątny w
taki sposób, że dolna podstawa graniastosłupa jest zawarta w podstawie stożka, a wierzchołki
górnej podstawy należą do powierzchni bocznej stożka.
Jaką największą objętość może mieć ten graniastosłup?
16 mar 15:17
janek191:
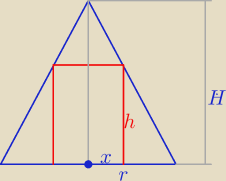
r = 2
√2
H = 5
Mamy
| 5 | | 2√2 | | 5√2 x | |
| = |
| ⇒ h = 5 − |
| |
| h | | 2√2 − x | | 4 | |
Dokończ

16 mar 15:48
madzia: czyli rozwiązujemy to tak, jakbyśmy do środka wpisali walec?
16 mar 17:38
madzia: i czym jest x? połowa przekątnej podstawy czy połowa boku podstawy?
16 mar 17:40
Mila:
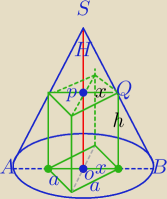
H=5
|OB|=r=2
√2
| | a√2 | |
x= |
| − połowa przekątnej kwadratu ( podstawy gran.) |
| | 2 | |
16 mar 18:58
 r = 2√2
H = 5
Mamy
r = 2√2
H = 5
Mamy

 H=5
|OB|=r=2√2
H=5
|OB|=r=2√2