stożek wpisany w walec 100onmywrist: Przekrój osiowy stożka jest trójkątem równobocznym o polu równym 9√3. W ten stożek wpisujemy walce w taki sposób, że jedna podstawa walca jest zawarta w podstawie stożka, a okrąg drugiej podstawy walca jest zawarty w polu powierzchni bocznej stożka. Wyznaczymy objętość tego walca, który ma największą objętość proszę o jakieś wskazówki

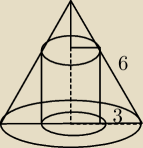
100onmywrist: czy tu trzeba skorzystać z zależnosci dwóch trójkątów prostokątnych?

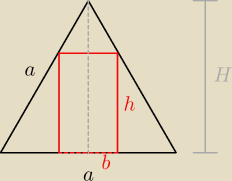
wredulus_pospolitus: 1) wyznaczasz 'a' oraz 'H' 2) z podobieństwa trójkątów:

H−h		b
	=
h		a   − b 2

z tego masz zależność pomiędzy h i b 3) V_walca = πb²*h szukasz maksimum

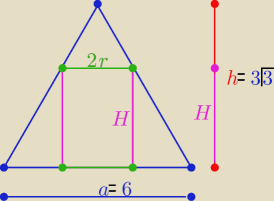
Eta: V_w=πr²*H Dla trójkąta równobocznego : a=6 , h=3√3 Z podobieństwa trójkątów

6		h
	=		⇒ H=√3(3−r) , r∊(0,3)
2r		h−H

V_w(r)= √3πr²(3−r) V^'(r)=.................. .....................

100onmywrist: Werudius pospolitus, ciezko mi tą zależność obliczyć tak szczerze, nie moge jakos tego pogrupować, masz pomysl jak to policzyc?

100onmywrist: ETA DZIĘKUJE <3 odp to 4√3

wredulus_pospolitus:

3√3 − h		b
	=
h		3−b

(3√3−h)(3−b) = h*b 9√3 − 3h + hb − 3b√3 = hb 9√3− 3b√3 = 3h h = √3(3 − b)

wredulus_pospolitus: i popatrz ... wyszła ta sama proporcja co u Ety

100onmywrist: wredulus pospolitus zwracam honor, nie zauważyłem, że hb się skróci, dziękuje równiez za pomoc!