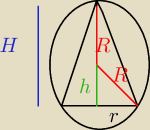
Oblicz objetosc stozka Michał: W kulę o promieniu długości R wpisano stożek o maksymalnej objętości. Oblicz objętość tego stożka. h²+r²=R² h=√R²−r² H=h+r

	πr2*√R2−r2
V=
	3

Proszę o pomoc bo mam tu blokadę,wiem,że są wzory na pochodną z pierwiastka,ale chyba można tu zbadać funkcję podpierwiastkową,bo jest ściśle rosnąca tylko co potem?Oczywiście,jeśli robię te zadanie poprawnie

Jerzy: Coś ci się pomieszało w tym zadaniu.Przecież h nie jest wysokością stożka.

Michał: nie no h oznaczyłem jako wysokośc tego trojkata prostokatnego o bokach h,r,R.Wysokoscia stozka jest H=h+r

Michał: Chyba,że chodzi o to,że źle wyznaczyłem te H

Jerzy: W twoim wzorze na objętość podstawiłeś małe h

Michał:

	πr2*(√R2−r2+R)
aa faktycznie,jeszcze zle napisalem,H=h+R*.To będzie V=		.Co z tym
	3

dalej zrobić?

Mila:

	1
1) Vs=		π*r2*H
	3

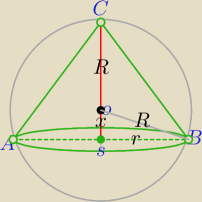
H=R+x, x∊(0,R) r²=R²−x² 2)Uzależniamy V_s od x. (aby uniknąć pierwiastka we wzorze)

	1
Vs(x)=		π*(R2−x2)*(r+x)
	3

3) Pochodna:

	1
V'(x)=		π*(−3x2−2xR+R2)
	3

V'(x)=0 Δ=16R²

	2R−4R		1		2R+4R
x1=		=		R lub x2=		<0 nie odp. założeniom
	−6		3		−6

	1		1
x=		R dla x=		R funkcja V(x) ma największą wartość
	3		3

( napisz dlaczego) 4) Objętość:

	1		8
r2=R2−		R2=		R2
	9		9

	1		4R
H=		R+R⇔ H=
	3		3

	1		8		4R
Vs=		π*		R2*
	3		9		3

	32π
Vs=		R3
	81

=========== Posprawdzaj rachunki

Michał: Dzieki za pomoc

Mila: