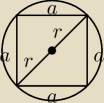
Prawdopodobieństwo nestor: Mamy kwadrat wpisany w okrąg. Jakie jest prawdopodobieństwo, że losowo wybrany punkt, znajdzie się w obszarze kwadratu. Tutaj mój rysunek poglądowy. Oczywiście prawdopodobieństwo P(A) będzie wynosiło pole kwadratu / pole koła, gdzie A to pole kwadratu, a Ω to pole koła, jednak w jaki sposób dokładnie to wyliczyć? Ponieważ wiem, że da się podać tutaj konkretny wynik

ICSP: a√2 = 2r ⇒ a = √2r i licz pole koła w zależności od r oraz pole kwadratu w zależności od r.

nestor:

	(√2r)2		2r2		2
Dziękuję! W takim razie P(A) =		=		=
	πr2		πr2		π

A jeszcze pytanko, jak z notacją, wystarczy napisać: Ω = {πr² ∊ R²} A = {a² ∊ R²} czy jakoś inaczej?

nestor: ICSP ?

ICSP: a² to jest liczba a nie element przestrzeni R². Tak samo πr². nawet nie wprowadziłeś układu.

nestor: W takim razie nie wiem jak z notacją

ICSP: Opisz słownie.

nestor: Wydawało mi się że można tak oznaczać. W innym zadaniu na spokojnie można było oznaczać Ω = {(x,y) ∊ R² : 0 ≤ x ≤ 1 /\ 0 ≤ x ≤ 2}. Tutaj żadnych wartości liczbowych podanych nie mam, żadnych warunków też nie.

ICSP: Jeżeli umieściłeś swój rysunek na płaszczyźnie to możesz wprowadzać pewne oznaczenia. Na chwilę obecną dwój rysunek wisi gdzieś w przestworzach.