trójkąt matura19: W trójkącie ostrokątnym ABC, AC<AB punkt S jest środkiem boku AB oraz CD jest wysokością Na boku BC wybrano taki punkt E że kąty CAE i CBA mają równe miary Z punktu D poprowadzono prostą prostopadłą do BC która przecięła prostą AE w punkcie M Wykaż że |DS|=|MS| Nie mam pomysłu jak to wykazać? pomożecie?

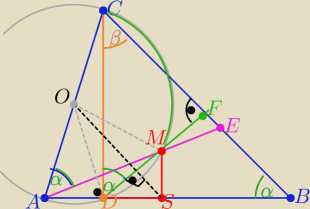
Eta: 1) trójkąty DFC i DBC podobne z cechy(kkk) to na czworokącie ADMC da się opisać okrąg ( bo kąty α są wpisane oparte na łuku MC średnicą tego okręgu jest bok AC bo kąt ADC=90^o i promienie |OD|=|OM| zatem OS jest środkową ΔABC więc OS∥BC to OS⊥DE bo OE⊥BC czyli OS jest symetralną odcinka DM zatem |DS|=|MS| =============== c.n.w.