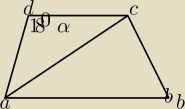
Stereometria Olek: Podstawą ostrosłupa jest trapez równoramienny o kącie ostrym α, w którym ramię i krótsza podstawa ma długość a. Każda krawędź boczna ostrosłupa tworzy z płaszczyzną podstawy kąt β. Oblicz objętość tego ostrosłupa Mam pytanie, czy mój sposób jest dobry. Ponieważ wszystkie krawędzie boczne tworzą równe kąty z podstawą to spodkiem wysokości ostrosłupa jest środek okręgu opisanego na podstawie. 1) Promień okręgu opisanego na trójkącie adc jest równy promieniowi opisanemu na trapezie

	α
2) kąt przy d to 180−α, a kąty <dac i <acd są równe		, AD=DC=BC=a
	2

3) Z tw. sin w ΔADC

a
	=2R /:2
α   sin   2

	a
R=
	α   2sin   2

I tu mam pytanie czy dobrze wyznaczyłem promień, czy tak nie wolno?

Olek: Mógłbyś ktoś pomóc?

Olek: :(

iteRacj@: Promień jest obliczony prawidłowo.

iteRacj@: P_p − pole podstawy

	1
Pp=		(a+a+2a*cos α)*a*sin α=(a+a*cos α)*a*sin α
	2

H − wysokość ostrosłupa H=R*tg β V − objętość tego ostrosłupa

	1		a
V=		*(a+a*cos α)*a*sin α*		*tg β
	3		2sin(α/2)