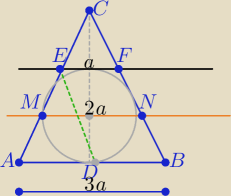
 1/Z treści zadania P(EFC): P(EFMN) : P(MNAB)= 1:3:5
wynika że P(ΔEFC) : P(ΔMNC) : P(ΔABC) = 1:4:9
to |EF| : |MN|: |AB|= 1:2:3 ( sam odpowiedz dlaczego?
więc |EF|=a , |MN|=2a , |AB|=3a
2/ czworokąt ABFE jest trapezem równoramiennym z wpisanym okręgiem
zatem z warunku wpisania okręgu w trapez mamy:
a+3a=|AE|+|BF| i |AE|=| BF|
to |AE|=|BF|=2a
dorysowujemy odcinek DE ∥FB otrzymujemy trójkąt ADE podobny do EFC
w którym |AE|=|FB|=|ED|=2a i |AD|= |AB|−|EF|= 3a−a= 2a
zatem ΔADE jest równoboczny
to i trójkąt ABC też jest równoboczny
c.n.w.
1/Z treści zadania P(EFC): P(EFMN) : P(MNAB)= 1:3:5
wynika że P(ΔEFC) : P(ΔMNC) : P(ΔABC) = 1:4:9
to |EF| : |MN|: |AB|= 1:2:3 ( sam odpowiedz dlaczego?
więc |EF|=a , |MN|=2a , |AB|=3a
2/ czworokąt ABFE jest trapezem równoramiennym z wpisanym okręgiem
zatem z warunku wpisania okręgu w trapez mamy:
a+3a=|AE|+|BF| i |AE|=| BF|
to |AE|=|BF|=2a
dorysowujemy odcinek DE ∥FB otrzymujemy trójkąt ADE podobny do EFC
w którym |AE|=|FB|=|ED|=2a i |AD|= |AB|−|EF|= 3a−a= 2a
zatem ΔADE jest równoboczny
to i trójkąt ABC też jest równoboczny
c.n.w.
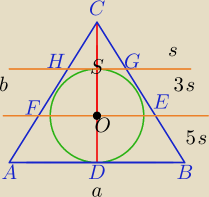 P=9s− pole ΔABC
AB=a, |BC|=|AC|=b
Stosunek pół figur podobnych jest równy kwadratowi skali podobieństwa
P=9s− pole ΔABC
AB=a, |BC|=|AC|=b
Stosunek pół figur podobnych jest równy kwadratowi skali podobieństwa
| 1 | 1 | |||
1)ΔHGC∼ΔABC⇔k2= | ⇔k= | |||
| 9 | 3 |
| 1 | 1 | 1 | ||||
|HG|= | a , |CG|= | b,|CH|] | b | |||
| 3 | 3 | 3 |
| 4 | 2 | |||
2)ΔFEC∼ΔABC⇔k12= | ⇔k1= | |||
| 9 | 3 |
| 2 | 2 | 2 | ||||
|FE|= | a, |CE|= | b, |CF|= | b | |||
| 3 | 3 | 3 |
| 2 | ||
GB|=|AH|= | b, | |
| 3 |
| 1 | 2 | 2 | ||||
a+ | a= | b+ | b | |||
| 3 | 3 | 3 |
| 4 | 4 | ||
a= | b⇔ | ||
| 3 | 3 |