 mam takie zadanie:
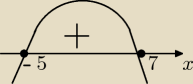
Wyznacz dziedzinę funkcji f(x) = √−x2 + 2x + 35. Podaj jej wartość największą.
Zrobiłem tak:
−x2 + 2x + 35 ≥ 0
x2 − 2x − 35 ≤0
Δ = 4 − 4 * (−35) = 4 − 140 = 144
√Δ = 12
mam takie zadanie:
Wyznacz dziedzinę funkcji f(x) = √−x2 + 2x + 35. Podaj jej wartość największą.
Zrobiłem tak:
−x2 + 2x + 35 ≥ 0
x2 − 2x − 35 ≤0
Δ = 4 − 4 * (−35) = 4 − 140 = 144
√Δ = 12
| −2−12 | ||
x1 = | = 7 | |
| −2 |
| Δ | ||
Kiedy obliczał wartość max ze wzoru yw = | wychodzi tyle ymax = 3 | |
| 4a |
| −Δ | −Δ | −12 | ||||
yw = | = | = | = 3 | |||
| 4a | −4 | −4 |
| −b | ||
Natomiast kiedy chcę obliczyć z takiego wzoru, gdzie yw = f(p), gdzie p to xw = | ||
| 2a |
| −b | ||
f(x) osiąga max dla xw= | = 1
| |
| 2a |
