czworokat
6latek:
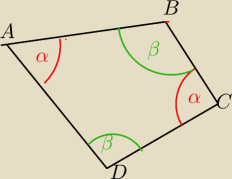
W wypuklym czworokacie ABCD zachodza zwiazki
AB=CDi kat DAB= katowi CDA wykaz ze
a) kąt ABC= kątowi DCB
b) czworokat ABCD jest trapezem
14 mar 10:10
6latek:
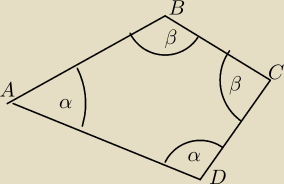
Zle oznaczenia katow na rysunku
14 mar 10:18
ite: Witaj, ja zawsze staram się rysować tak, żeby równe odcinki wyglądały na "mniej więcej" równe.
Łatwiej wtedy szukać rozwiązania.
14 mar 10:22
mat : Uznając za podstawę AD, mamy trapez rownoramienny
14 mar 10:24
6latek: Dzien dobry

Wlasnie tak sobie pomyslalem zeby teraz narysowac w zeszycie linijka i katomierzem
Zaraz to zrobie
14 mar 10:24
ite: @mat ale chodzi teraz o to żeby to udowodnić
14 mar 10:27
mat : Tzn mnie się to wydaje trywialne. Opuścić wysokość z B i C i udowodnić że są tej samej
długości, np.z podobieństwa trójkątów
14 mar 10:29
6latek:
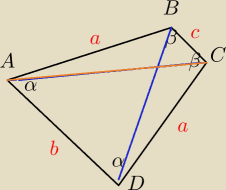
Pomysle bo musze to zrobic z przystawania trojkatow (a)
14 mar 10:53
mat : Jak najbardziej z przystawania

14 mar 11:12
ite: To dokładnie tak jak napisał mat, wysokości wyznaczą trójkąty podobne i to w skali 1:1. I
możesz rozważyć przypadki w zależności od kąta α, żeby nie było za szybko : )
14 mar 11:15
6latek: Z przystawania trojkatow ABD i ACD (cecha BKB) mam ze AC=BD
Z ptrzystawania tych trojkatow mam ze kąt ABD= kątowi ACD
mam jeszcze dwa trojkaty przystajace ΔABC i BCD
AC=BD
AB=DC
Teraz brakuje mi 3 cechy bo naprade bedzie ze bok BC bedzie rowny dla obu trojkatow
Z przystawania tych trojkatow bede mial ze kąt ACB= kątowi DBC
Wtedy kąty β sa rowne
14 mar 11:19
6latek: ite
Pytanie . czy podobienstwo jest w 1 klasie liceum ?
14 mar 11:20
6latek: Prosze zeby ktos odpowiedzial mi jakiej tej 3 cechy brakuje
14 mar 11:38
ite:
ΔABC i ΔBCD to trójkąty przystające na podstawie (bbb) ⇒ |<ABC|=|<DCB|
14 mar 11:52
6latek: Dlaczego BBB?
14 mar 11:54
6latek: Wiesz dwa boki mam tylko dlaczego trzeci ?
14 mar 11:54
ite:
W jedynym podręczniku do szkoły średniej, który mam (wydawnictwa Pazdro) podobieństwo jest w
klasie 1. Czyli jest w programie. W której klasie jest w innych podręcznikach, to wiedzą
nauczyciele, może odpowiedzą.
14 mar 11:56
6latek: Czyli bede musia sie wziac porzadnie za to podobienstwo i Talesa . Dobrze
14 mar 11:59
ite: Równość AC=BD wykazałeś 11:19. Do cechy przystawania kbk lub bkb nie znasz równości potrzebnych
tamch kątów.
14 mar 11:59
6latek:
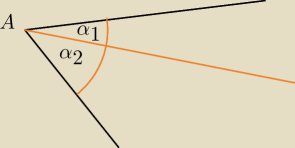
Teraz sobie pomyslalem ze jakbym ten kat α podzielil np na dwa kąty na rysunku
wtedy zapisal ze α
1+α
2=α
Wtedy mialbym BKB
Wtedy przy podstawie rowne kąty z przystawania trojkatow BC rownolegle do AD i trapez
rownoramienny
14 mar 12:07
6latek: Zaraz uciekam bo o 14: 30 jade z rodzicami do ortopedy
Nie wiem kiedy wroce . Pewnie gdzies kolo 19 ,Wtedy dam inne zadanka . Do zobaczenia

14 mar 12:11
ite:
Z przystawania trójkątów ΔABD i ΔACD wynika, że ten kąt α2 jest kątem i w ΔABC i w ΔBCD, wtedy
można skorzystać z BKB. Ale więcej pisania niż skorzystanie z BBB.
14 mar 12:18
14 mar 13:09
6latek: Jednak jedziemy o 15 wiec troche sobie jeszcze posiedze .
14 mar 13:46
 W wypuklym czworokacie ABCD zachodza zwiazki
AB=CDi kat DAB= katowi CDA wykaz ze
a) kąt ABC= kątowi DCB
b) czworokat ABCD jest trapezem
W wypuklym czworokacie ABCD zachodza zwiazki
AB=CDi kat DAB= katowi CDA wykaz ze
a) kąt ABC= kątowi DCB
b) czworokat ABCD jest trapezem
 Zle oznaczenia katow na rysunku
Zle oznaczenia katow na rysunku
 Wlasnie tak sobie pomyslalem zeby teraz narysowac w zeszycie linijka i katomierzem
Zaraz to zrobie
Wlasnie tak sobie pomyslalem zeby teraz narysowac w zeszycie linijka i katomierzem
Zaraz to zrobie
 Pomysle bo musze to zrobic z przystawania trojkatow (a)
Pomysle bo musze to zrobic z przystawania trojkatow (a)

 Teraz sobie pomyslalem ze jakbym ten kat α podzielil np na dwa kąty na rysunku
wtedy zapisal ze α1+α2=α
Wtedy mialbym BKB
Wtedy przy podstawie rowne kąty z przystawania trojkatow BC rownolegle do AD i trapez
rownoramienny
Teraz sobie pomyslalem ze jakbym ten kat α podzielil np na dwa kąty na rysunku
wtedy zapisal ze α1+α2=α
Wtedy mialbym BKB
Wtedy przy podstawie rowne kąty z przystawania trojkatow BC rownolegle do AD i trapez
rownoramienny
