Stereometria graniastosłup przecięty płaszczyzną
bfs: Graniastosłup prosty ABCDEFGH, którego podstawą jest równoległobok ABCD o długośći |BC| = 10,
|DC| =14 przecięto płaszczyzną BGD. Oblicz jaką częścią objętości graniastosłupa jest
objętość każdej z brył, na które płaszczyzna przekroju podzieliła graniastosłup, jeżeli |BD| =
12
13 mar 23:31
wredulus_pospolitus:
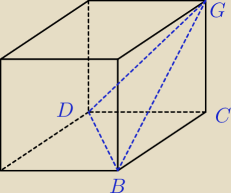
zauważ, że płaszczyzna BGD dzieli podstawę 'na pół'
| | 1 | | 1 | |
więc bez obliczania czegokolwiek ... VBCDG = |
| * |
| VABCDEFGH |
| | 2 | | 3 | |
| | 1 | | 5 | |
Więc ów płaszczyzna dzieli objętość tego graniastosłupa na części: |
| V ; |
| V |
| | 6 | | 6 | |
Jak widzisz ... długości boków i przekątnej są tutaj całkowicie zbyteczne
13 mar 23:54
bfs: wreduluspospolitus czemu 13 * VABCDEFGH
14 mar 00:07
wredulus_pospolitus:
V
ABCDEFGH = P
ABCD*H
| | 1 | | 1 | | 1 | |
Vostrosłupa = |
| PDBC*H (wzór na objętość ostrosłupa) = |
| * |
| PABCD*H |
| | 3 | | 3 | | 2 | |
| | 1 | |
I stąd wiemy, ze Vostrosłupa = |
| VABCDEFGH |
| | 6 | |
14 mar 00:14
bfs: dzięki
14 mar 00:17