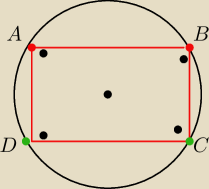
Okrag i czworokat 6latek: Przez dwa dane punkty A i B okregu o(O,r) prowadzimy proste prostopadle do AB przecinajace okrag odpowodnio w punktach D i C Wykaz ze jesli punkty nie sa koncami jednej srednicy to czworokat ABCD jest prostokatem na czworokacie mozna opisac okrag jesli suma przeciwleglych kataow wynosi 180^o Wobec tego kąty C i D maja po 90^o Takie byloby moje rozwiazanie jednak w podpowiedzi mam aby wykazac ze AC i DB sa srednicami okregu

Pytający: ΔABC jest trójkątem prostokątnym (wynika to z opisu zdania) i jest on wpisany w okrąg. Stąd wynika, że AC jest średnicą. Analogicznie dla trójkąta ACD.

6latek: OK. Juz widze

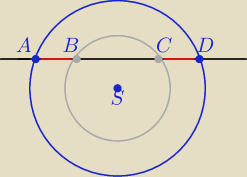
Eta: Wykaż,że |AB|=|DC|

6latek: Przepraszam ogladalem film Juz probuje Jesli ze srodka tych okregow poprowadze prosta prostopadla do siecznej AD to to prosta podzieli kazda z cieciw na polowy Wniosek |AB|=|CD|

wredulus_pospolitus: 6latek ... tak ... ale Ty stwierdziłeś, że ów prostopadła podzieli sieczne na pół ... a musisz to pokazać (wystarczy napisać jedną rzecz )

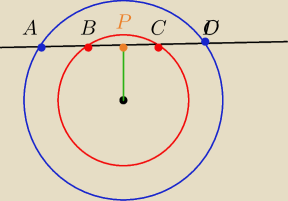
6latek: PB=PC PA=PD PA−PB=AB PD−PC=CD=AB Tak powinno byc dobrze Eta

6latek: wredulus a co nalezalo napisac ?

6latek: No nic dobranoc rano zobacze .

wredulus_pospolitus: A skąd wiesz, że PB = PC ? Na jakiej podstawie to? Brakuje jednego stwierdzenia, a nim jest: ΔOBC jest równoramienny ... więc OP jako wysokość sprawia, że PB = PC Analogicznie AP = PD I robisz tą różnicę.

6latek: Dobrze