Funkcje liceum czarek12: Witam, takie zadanko mam Funkcja homograficzna F jest monotoniczna w przedziałach (−∞,0) i (0, ∞) Zbiór R − {3} jest zbiorem wartości tej funkcji, a wartość 5 funkcja przyjmuje dla argumentu 3 1. Znajdź wzór funkcji 2. Wyznacz miejsce zerowe 3. Wyznacz argumenty, dla których funkcja przyjmuje wartości większe od 1 Co do samego polecenia, to f(3) = 5, tak? Ale co mi to daje? Nie mam kompletnie pomysłu jak zacząć

wredulus_pospolitus: nie może być f(3) = 5 ... skoro x=3 NIE NALEŻY DO DZIEDZINY FUNKCJI

Eta: hiperbola : i z treści zadania :

	a
f(x)=		+3 bo x=0 asyptota pionowa i y=3 asymptota pozioma
	x

	a
f(3)=5 ⇒		+3=5 ⇒ a=6
	3

	6
f(x)=		+3 , x≠0
	x

=========== b) f(x)=0 ⇒ .................. c) f(x)>1 ⇒ ............ dokończ

wredulus_pospolitus: ach nie ... zbiór funkcji ... oki ... cofam co napisałem

Eta: Czytanie ze zrozumieniem ZW= R\ {3}

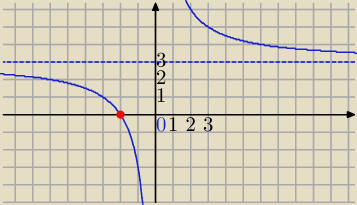
Mila: y=3 asymptota pozioma ( ze zbioru wartości) x=0 asymptota pionowa ( Z dziedziny, x=0 ∉D)

	a
f(x)=3+
	x

	a
3+		=5
	3

a
	=2
3

a=6

	6
f(x)=3+		resztę spróbuj sam
	x

czarek12: dziękuję bardzo za pomoc