trójkat ohja: Skonstruj trójkat o wierzchołkach A, B, C, gdzie BC=7,5cm, kat ABC=45 oraz AB−AC=1cm.

wredulus_pospolitus: Z czego potrafisz korzystać ? Znasz tw. cosinusów ?

wredulus_pospolitus: Posiadasz cyrkiel ?

ohja: znam tw cosinusów

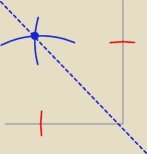
wredulus_pospolitus: No dobra, więc: 1) najpierw (za pomocą cyrkla i ekierki) wyznaczymy kąt 45^o (nie oszukujemy pomagając sobie kratkami w zeszycie ) 2) za pomocą ekierki rysujemy kąt prosty 3) bierzemy cyrkiel do łapki i zaznaczamy na bokach łuki (dowolny − ale ten sam promień) 4) wbijamy w te punkty i znowu zaznaczamy łuki, tym razem 'pomiędzy' bokami (promień 'dowolny', byleby nie za mały) 5) ich przecięcie daje nam drugi punkt 6) i mamy kąt 45^o

wredulus_pospolitus: 'podstawą' będzie BC ... ekierką odmierzamy 7.5 cm i teraz pora na rachunki: |AB| − |AC| = 1 cm −> |AB| > |AC| oznaczmy |AC| = x , wtedy |AB| = x+1 więc z tw. cosinusów: x² = (x+1)² + (7.5)² − 2*(x+1)*7.5*cos(45^o) wyznaczasz 'x'. Mając 'x' odmierzasz długość na cyrku, cyrkiel wbijasz w wierzchołek C i zataczasz łuk ... przecięcie się łuku z wyznaczoną wcześniej prostą (będącą pod kątem 45^o do podstawy BC) będzie da nam ostatni wierzchołek.

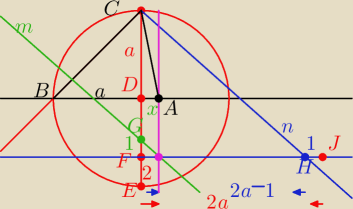
an: To ma być rysunek konstrucyjny, a nie jakieś przedszkole.

	7,5
a=		cm ;CA=a+x−1
	√2

	2a−1
x=
	2a−2

konstrujemy dwie proste przecinające sie pod katem 90_o następnie sieczną i mamy dwie proste pod ∡45_o przecnające się w B odmierzamy odcinek BC=7.5cm z punktu C prowadimy prostopadłą do drugiego ramienia mamy punkt D, BD=CD mamy trójkąt CDA o wymiarach zgodnie z treścią zadania wyliczamy x jw. Teraz musimy skonstruować odcinek x o wyliczonej długości Okrąg ma r=a ; CF=2a−2 ; FH=2a−1;HJ=1;EF=2; GF=1 , m||n konstrukcji prostopadłych i równoległych nie pokazuje gdyż sa to "podstawowe podstawy" i zaciemnią rysunek