pochodna pochodna :

	−8
Mam wyznaczyć ekstrema lokalne, pochodna ma wzór: f'(x)=		+ 2x
	x3

Df'(x)=Df(x)= R\{0} jak to zrobić?

Asia: http://www.naukowiec.org/wiedza/matematyka/ekstremum-funkcji-minimum-maksimum-_677.html

Asia: nmzc

pochodna : znam ogólny schemat, chodzi mi o ten szczególny przykład, dlatego, że wychodzi mi zła odpowiedź

jc: Dla x>0, mamy sumę dwóch funkcji rosnących, więc ekstremum żadnego nie będzie. Funkcja jest nieparzysta, więc dla x<0 też nie będzie ekstremum.

Jerzy: Pokaż funkcję.

pochodna :

	4
f(x)=		+ x2 + 5
	x2

jc: Ach, bo to była pochodna, nie funkcja.

	4
f(x)=x2+		+ C
	x2

Funkcja ma minima lokalne w punktach ±√2.

pochodna : W odpowiedziach jest: f'(x)<0 ⇔ x ∊ (−∞, √2 ) i (0, √2 ) f'(x)>0 ⇔ x∊( −√2, 0) i (√2, +∞)

pochodna : i nie rozumiem, dlaczego 0 jest tutaj traktowane, jakby również było pierwiastkiem? bo to wynika z przedzialów

pochodna : ktoś ma pomysł

Jerzy: Przecież 0 nie należy do dziedziny tej funkcji.

pochodna : Wiem, że nie należy, ale nie rozumiem skąd w takim razie wynikają te przedziały

Jerzy: Z miejsc zerowych pochodnej i tam są ekstrema lokalne.

pochodna : Ale 0 jest tutaj ekstremum?

wredulus_pospolitus: ze względu na postać pochodnej:

	x2 − 4
f'(x) = 2
	x3

zauważ, że mianownik bywa także ujemny czyli wpływa na znak pochodnej dlatego 0 jest uwzględniany jako jeden z pieriwastków

	1
Analogiczna sytuacja będzie dla g(x) =
	x2

oczywiście x=0 nie należy do dziedziny funkcji, ale jak policzysz pochodną to okaże się, że dla x<0 masz f' >0 natomiast dla x>0 masz f'<0

wredulus_pospolitus: celowo podałem taką funkcję za przyklad, bo (mam taką nadzieję) raczej wiesz jak wygląda wykres tejże funkcji.

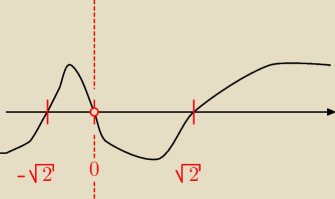
wredulus_pospolitus: a wracając do Twojego zadania

	x2−2
f' = 2		> 0 ⇔ 2(x2−2)*x > 0 (pomnożyłem przez x4)
	x3

więc mamy (metoda wężyka) taki szkic wykresu

pochodna : O, właśnie o taką odpowiedź mi chodziło dziękuję, nie miałam o tym dotychczas pojęcia i nie uwzględniałam nigdy 0. W takim razie w takich przypadkach po narysowaniu szkicu monotoniczności takiej funkcji wykres zawsze będzie przecinał 0, tak?

pochodna : Nie zauważyłam tej ostatniej odpowiedzi. O to mi dokładnie chodziło, bardzo bardzo dziękuję!

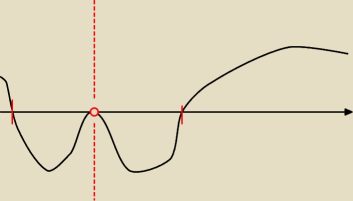
wredulus_pospolitus: Nie zawsze będzie przecinał zero

	x2−2
np. gdyby f'(x) =		i byś nie zauważyła że mianownik jest zawsze dodatni i
	x2

po przemnożeniu przez 'kwadrat mianownik' (bo tak standardowo uczą nas mnożyć w nierównościach, jak 'nie znamy znaku' ) otrzymałabyś: f'(x) = (x²−2)*x² i w tym momencie (zgodnie z zasadą z metody wężyka) szkic by wyglądał tak

wredulus_pospolitus: PS. I dlatego polecam zawsze robić sobie szkic wykresu pochodnej ... niewiele czasu zajmie, a mocno ułatwia sprawę

wredulus_pospolitus: PS. Warto też (dla świętego spokoju) też sobie w pamięci policzyć granice pochodnej w +∞ oraz w −∞ (a raczej ... pomyśleć czy będzie dodatnia czy ujemna), w tym momencie szybko sprawdzimy czy aby nie zrobiliśmy błędu (co nie znaczy że mam 100% pewność, że dobrze zrobiliśmy )

pochodna : Z reguły trafiały mi się właśnie takie przykłady z x² w mianowniku, dlatego myślałam, że właśnie tak jak tutaj ten wykres nigdy nie będzie przecinał 0. U góry napisałam o tym, że zawsze przecina, ale chodziło mi o tę sytuację z samym x albo nieparzystą potęgą przy x w mianowniku. Jeszcze raz dziękuję

wredulus_pospolitus: I gdybyś właśnie policzyła te granice pochodnej to byś zauważyła, że 'coś jest nie tak' (w Twoim pierwotnym rozwiązaniu)

wredulus_pospolitus: To jeszcze taka jedna uwaga. Nie wiem na ile prowadzący się tego może czepiać (ja bym się czepiał).

	x2 − 4
Jeżeli masz przykładowo f' =
	x4

i później robisz nierówność x²−4 > 0 to wcześniej warto by było dodać komentarz: " ∀{x∊D_f' x⁴ > 0 " Taki komentarz oznacza, że ja wiem, że Ty wiesz dlaczego 'olałaś' mianownik