funkcja Ateusz: Wyznacz wszystkie wartości parametru m, dla których zbiór rozwiązań nierówności

	1
|		−5| ≥ m
	3x−2

jest przedziałem postaci (−∞, a> Wiem jak będzie wyglądać funkcja, jestem w stanie poprawnie naszkicować jej wykres, ale co z tym przedziałem? Co to jest to a? Jakaś niewiadoma czy współczynnik przed x czy co?

wredulus_pospolitus: parametr m będzie uzależniony od a będziemy mieli: f_min(x) = f(a) = m

Mila:

	1
f(x)=|		−5|
	3x−2

	1
f(0)=|		−5|=4
	3−2

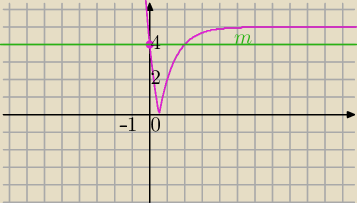
	1
|		−5|≥4 dla x∊(−∞,0>
	3x−2

iteRacj@: Milu czy rozwiązaniem nierówności z 18:56 nie powinno być x∊(−∞,0>U<2,∞) ? A zbiór rozwiązań wyjściowej nierówności będzie przedziałem postaci (−∞, a> dla wartości parametru m≥5 ?

Mila: Tak masz rację. Trzeba wyżej przesunąć prostą. Coś mi się ubzdurało, że nie f(x) nie przyjmuje wartości 5. Napisz całe rozwiązanie. Pozdrawiam

Ateusz: eh nadal nie czaje co to jest to a?

Mila: Pofatygowałeś się , aby przeczytać, to co napisała Iteracja ?

	1
f(x)=|		−5|
	3x−2

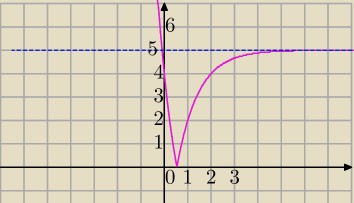
Masz znaleźć takie m dla którego wykres f(x) leży powyżej prostej y=m powyżej prostej y=5 leżą wszystkie wartości f(x) dla pewnych x−ów. f(a)=5

	1
|		−5|=5
	3x−2

1		1
	−5=5 lub		−5=−5
3x−2		3x−2

1		1
	=10 lub		=0 brak rozw.
3x−2		3x−2

1
	=3x−2
10

−log₃(10)=x−2 x=2−log₃(10) Dla x≤2−log₃(10) wartości f(x)są większe od 5 lub równe 5. ⇔

	1
|		−5|≥5 dla x∊(−∞,2−log3(10) >
	3x−2

a=2−log₃(10) to jest koniec przedziału. Należy interesować się wcześniej rozwiązaniem. Przypadkowo zobaczyłam, że masz dalej problem.