dowod geo
Ateusz: W trójkącie ABC poprowadzono środkową CD i wyznaczono na niej taki punkt E, że
| | CP | | 1 | |
.Prosta przechodząca przez punkty AE przecina bok BC w punkcie P. Wykaż, że |
| = |
| |
| | PB | | 6 | |
Nie mam pojęcia...
.
13 mar 18:02
wredulus_pospolitus:
A rysunek zrobiony chociaż

13 mar 18:05
Ateusz:
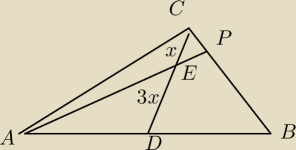
13 mar 18:10
Mila:
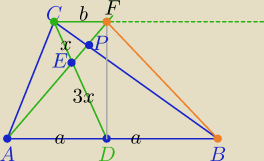
Jeden ze sposobów:
CF||AB)
1) W trapezie ADFC:
| | b | | x | |
ΔCFE∼ΔADE w skali k= |
| = |
| ⇔ |
| | a | | 3x | |
W trapezie ABFC :
| | b | | b | | 1 | |
ΔCPF∼ΔABP w skali k1= |
| = |
| = |
| ⇔ |
| | 2a | | 2*3a | | 6 | |
============
13 mar 18:43
Mila:
Eta ma jeszcze inny sposób, będzie to napisze

13 mar 18:44
13 mar 18:45
Eta:
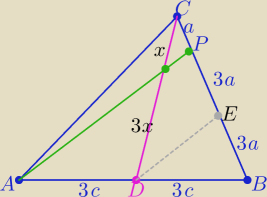
AP ∥ DE i z tw. Talesa wΔDEC |CP|=a i |PE|=3a
i z tw. Talesa w ΔABP |BE|=3a
to:
13 mar 19:38
Mila:

13 mar 19:58
Ateusz: sa jeszcze jakies inne sposoby?
slyszalem ze mozna cos z tw. sinusow np.
z calej geometrii to wlasnosci wynikajace z talesa jakos najslabiej do mnie przemawiaja
17 mar 12:54
Mila:
18:43 masz rozwiązane z zastosowaniem podobieństwa .
Własności trapezu musisz znać.
17 mar 19:03
Ateusz: 18:43
skąd wiemy, że odcinek EF ma w ogóle prawo bytu? Skąd wiemy, że p.prosta AE "wyceluje" akurat w
punkt F, który jest spodkiem środka dłuższej podstawy trapezu?
20 mar 19:49
Mila:
1) Rysujemy prostą przechodzącą przez C i równoległą do AB.
2)Prosta przechodząca przez punkty AE przecina bok BC w punkcie P z treści zadania.
Przedłużamy tę prostą do przecięcia z narysowaną równoległą i oznaczamy ten punkt przecięcia
jako F.
20 mar 20:02
Ateusz: czasem jest tak, ze wynajduje nieprawdziwe wlasnosci na rysunku, ktore znacznie ulatwiaja
zadanie, a nie maja prawa bytu, tutaj tez nie mamy pewnosci ze nawet jak przetne te linie to
trafie akurat w punkt F, bo np. trafie minimalnie obok i bede mogl tylko i wylacznie
podejrzewac, ze ta linia miala trafic w spodek srodka AB
20 mar 20:11
Mila:
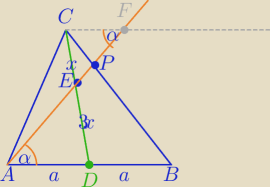
CF||AB
Przeczytaj uważnie to , co napisałam. 20:02.
Otrzymany punkt F łączysz ze środkiem.
Możesz zresztą jeszcze prościej>.
ΔCEF∼ΔADE
| CE | | 1 | | CF | | 1 | | CF | | 1 | |
| = |
| z treści zadania, to również |
| = |
| ⇔ |
| = |
| |
| ED | | 3 | | AD | | 3 | | a | | 3 | |
| | 1 | |
W takim razie : |CF|= |
| a |
| | 3 | |
Ponieważ ΔCFP∼ΔABP to również :
20 mar 20:50
Ateusz: dzieki, zrozumiale.
jeszcze jedno pytanie, jak mam w poleceniu wykazac cos wynikajacego ze stosunkow dlugosci
poszczegolnych bokow, to w 90% bardzo przydatne bedzie dorysowanie sobie czegos, tak jak
tutaj, po czym skorzystanie z trojkatow podobnych, tak jak tutaj, prawda?
20 mar 20:54
Mila:
No nie wiem, czy w 90% , ale często się przydaje.
20 mar 21:10


 Jeden ze sposobów:
CF||AB)
1) W trapezie ADFC:
Jeden ze sposobów:
CF||AB)
1) W trapezie ADFC:

 AP ∥ DE i z tw. Talesa wΔDEC |CP|=a i |PE|=3a
i z tw. Talesa w ΔABP |BE|=3a
to:
AP ∥ DE i z tw. Talesa wΔDEC |CP|=a i |PE|=3a
i z tw. Talesa w ΔABP |BE|=3a
to:

 CF||AB
Przeczytaj uważnie to , co napisałam. 20:02.
Otrzymany punkt F łączysz ze środkiem.
Możesz zresztą jeszcze prościej>.
ΔCEF∼ΔADE
CF||AB
Przeczytaj uważnie to , co napisałam. 20:02.
Otrzymany punkt F łączysz ze środkiem.
Możesz zresztą jeszcze prościej>.
ΔCEF∼ΔADE